1 Reactions, Reactors, and Reaction Engineering

Chemical reactions are molecular events that take place within chemical reactors, and chemical reactors are a focal point of reaction engineering. Consequently Reaction Engineering Basics begins with discussion of reactions, reactors and reaction engineering.

1.1 Chemical Reactions

1.1.1 Defining and Characterizing Chemical Reactions

A chemical reaction involves a group of atoms. Before the reaction occurs, there are bonds between some of the atoms, so that the system consists of one or more molecules and/or free atoms. Collectively, these chemical species are called the reactants. A chemical reaction is a molecular event wherein at least one chemical bond is broken or formed. As a consequence, after the reaction occurs, the system consists of a different set of chemical species. Collectively, these chemical species are called the products.

As an example Figure 1.1 shows a schematic representation of a system containing two oxygen atoms and four hydrogen atoms. In Figure 1.1 (a), the oxygen atoms are bonded to each other and each of the hydrogen atoms is bonded to one other hydrogen atom. As a result, there are three chemical species or reagents: an O₂ molecule and 2 H₂ molecules. If this is the state of a chemical system before a reaction occurs, this group of reagents could be referred to, collectively, as the reactants. When a chemical reaction occurs, the bonding between the atoms in the system changes. For example, Figure 1.1 (b) shows the same six atoms, but the bonding among them is different. Each of the oxygen atoms is bonded to two hydrogen atoms giving two chemical species both being water molecules. If this is the state of the chemical system after the reaction has occurred, then this group of reagents, collectively, is called the products.

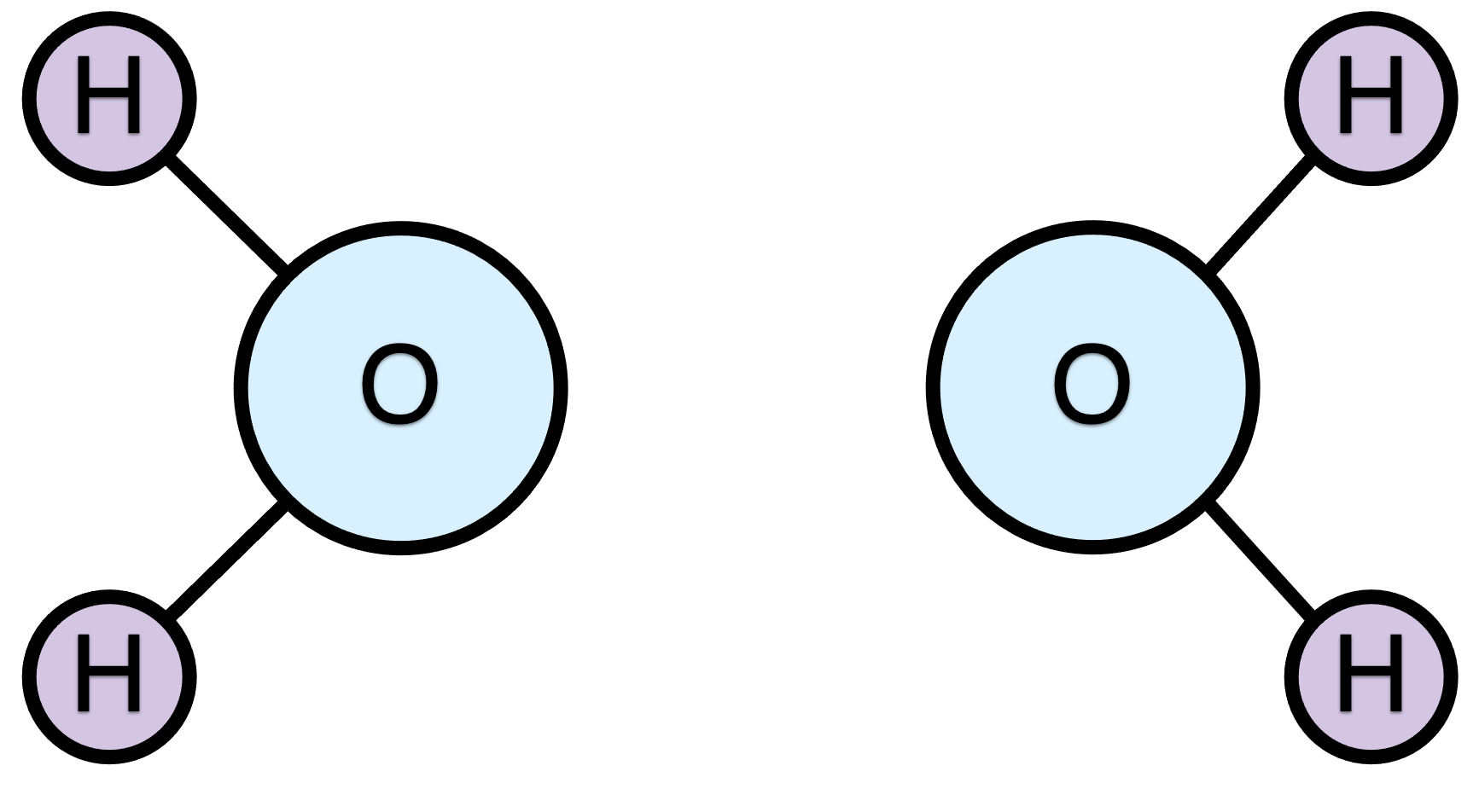
So to summarize the example, before the reaction, the chemical system consisted of three reactants: an O₂ molecule and two H₂ molecules. The reaction changed the bonding among the atoms, so that after the reaction the chemical system consisted of two species, the products, both being water molecules. It is very important to recognize that the exact same set of six atoms is present throughout the process. This is the basis of chemical reaction stoichiometry. Stoichiometry is examined in more detail in the next sub-section.

It’s important to understand that chemical reactions are bi-directional. In terms of the example here, a chemical system might initially contain two water molecules, and a chemical reaction could occur to produce one oxygen molecule and 2 hydrogen molecules. What that means, among other things, is that the identity of the reactants and the identity of the products is context specific. In one situation, two H₂O molecules might be the reactants with O₂ and two H₂ as the products, and in a different situation, O₂ and two H₂ might be the reactants and 2 H₂O, the products.

There is another very important subtlety to the definition of a chemical reaction as a molecular process that converts reactants into products, by changing the bonding among the atoms. Specifically, the issue is whether all the bonds break and form simultaneously, or, alternatively, whether the process occurs in more than one step. Figure 1.2 shows that same representation of the hydrogen combustion reaction, but with the reactant bonds that will break colored red and the bonds that will form colored green. This particular reaction is unusual in that every bond in the reactants breaks and four new oxygen-hydrogen bonds form.

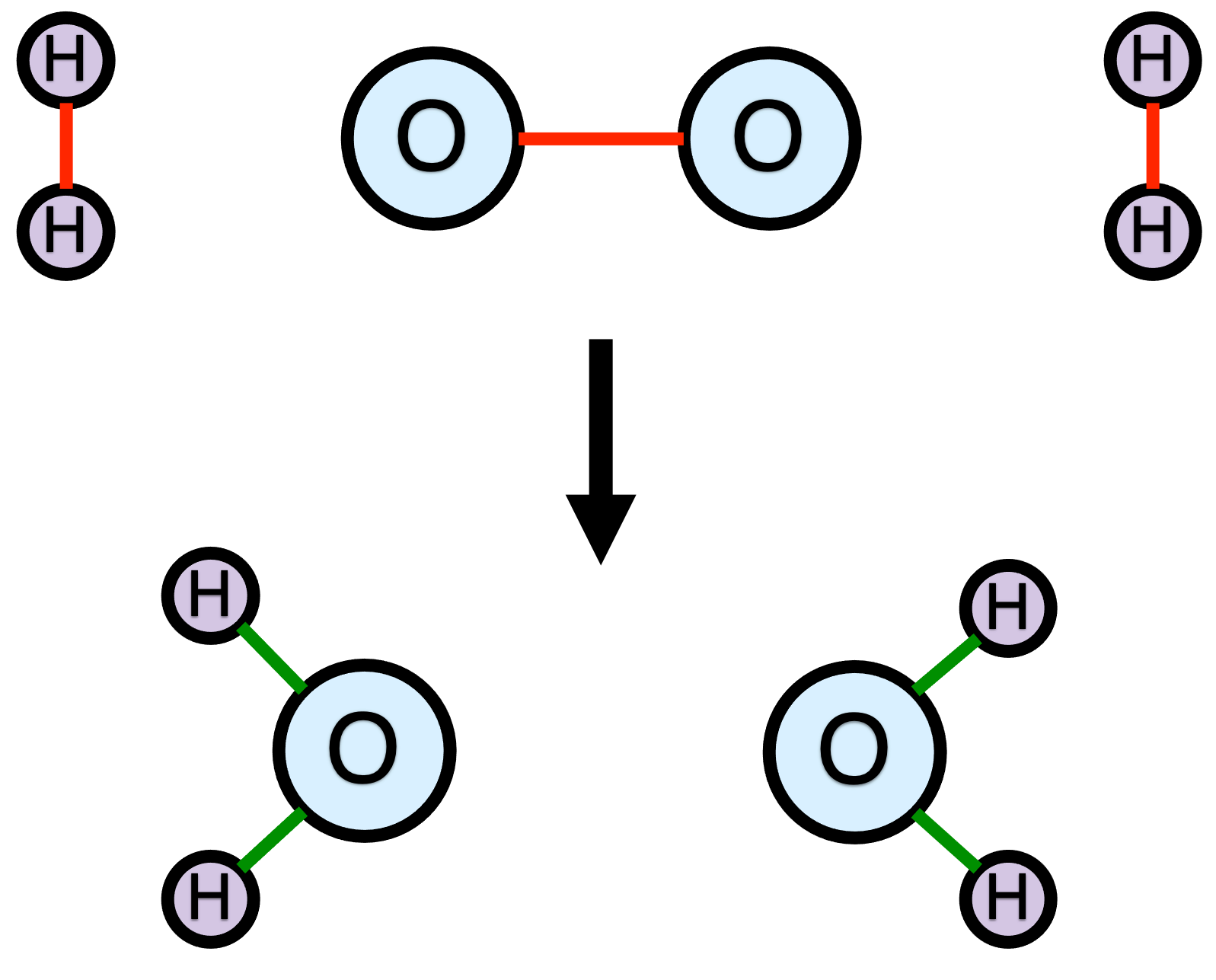
Figure 1.2: When molecular hydrogen is oxidized three bonds (red) break and four bonds (green) form.

If all of the bond breaking and forming occurs simultaneously, then this reaction would be called an elementary reaction. In an elementary reaction, all of the reactants come very close to each other, and all of the bonds that are going to do so begin to break or form. While this is happening, the system consists of a single species. That species is call the activated complex. The lifetime of the activated complex is extremely short. Even as the reactants are forming the activated complex, it is beginning to break apart into the products.

The alternative is that the bond breaking and forming is not simultaneous, but it occurs sequentially. Given the large number of bonds that are breaking and forming during hydrogen combustion, it is likely that they break and form sequentially. That would mean that hydrogen combustion is a non-elementary reaction. Instead of a single reaction event where all of the bonds break and form, the O₂ molecule and one of the H₂ molecules might react to form two hydroxyl radicals. Products like these hydroxyl radicals are often called intermediates or reactive intermediates. The reactive intermediates do not have to be free radicals, they also can be neutral species with all electrons paired or they can be ions. One key feature of the intermediates is that their lifetimes are very short compared to the lifetime of the reactants and products.

Continuing with hydrogen combustion, if the first step resulted in formation of two hydroxyl radicals, then those radicals would react very quickly. That might generate new intermediates, and they, too, would react quickly. The net result is that the reactants are converted to intermediates that, in turn, are very quickly converted to products. While the intermediates react very rapidly, they are present and could be detected using sophisticated equipment. As such, their lifetimes are longer than an activated complex in an elementary reaction, but still quite short.

Another way to look at the intermediates is to remember that from a macroscopic perspective it appears that the single non-elementary reaction is all that is happening. If the intermediates were present in significant quantity, then from a macroscopic perspective, they would be observed, and it would no longer appear that only one reaction was taking place. So while it appears that only one reaction is taking place from a macroscopic perspective, if one was able to observe the system at the microscopic or molecular level, it would be seen that actually more than one reaction was taking place and that the intermediates were being formed and consumed in those reactions.

It is worth noting that the number of reactant molecules participating in a chemical reaction event is used as one means of classifying reactions. If there is only one reactant in a chemical reaction event, that reaction can be referred to as a unimolecular reaction. If there are two reactants, either two of the same molecule or one each of two different molecules, the reaction can be referred to as a bimolecular reaction. A termolecular reaction has three reactant molecules. When a single molecule is the only reactant and there is also a single molecule as the only product, the reaction can additionally be called an intramolecular reaction. In an intramolecular reaction all bond breaking and forming is internal to the single molecule involved in the reaction. Other means of classifying reactions are described later in this chapter.

1.1.2 Chemical Reaction Stoichiometry

The preceding sub-section defined a chemical reaction as a molecular process wherein reactants were converted to products due to changes in the chemical bonding. The fact that the number of atoms and their identities do not change, but the bonding between them does change is the basis of chemical reaction stoichiometry. Before discussing stoichiometry, though, it may be worth noting that the word “reaction” has two meanings. One use of the word “reaction” refers to the molecular process as previously defined. But the word “reaction” is also used to refer to the written expression that is used to represent and describe that molecular process.

For example, in the preceding sub-section the word “reaction” was used to refer to a molecular bond breaking and forming process involving hydrogen and oxygen atoms. That process can be represented by the following expression.

\[ 2 H_2 + O_2 \rightarrow 2 H_2O \tag{1.1}\]

The word “reaction” is used to refer to the molecular event, and it is also used to refer to the expression, e. g. Reaction 1.1. In most circumstances, these two uses for the word “reaction” don’t cause any confusion. In this sub-section, however, they might. Therefore, for the remainder of this sub-section the phrase “molecular reaction event” will be used to refer to the molecular event and the phrase “reaction expression” will be used to refer to the expression representing that event.

Each time the molecular reaction event occurs the same number of molecules of each reactant is converted into the same number of molecules of each product. For example every time the hydrogen combustion molecular reaction event occurs, one O₂ molecule and two H₂ molecules are converted into two water molecules. The fixed proportions in which the reactants and products participate are referred to collectively as the stoichiometry of the reaction.

Here’s that reaction expression for hydrogen combustion again.

\[ 2 H_2 + O_2 \rightarrow 2 H_2O \]

In this case, the reaction expression contains an arrow that points to the right. To the left of the arrow the chemical formula for each unique reactant in the molecular reaction event is written. The chemical formulae of the reactants are separated by plus signs, and each is preceded by the number of molecules of that species that participates in the molecular reaction event. If no number precedes the chemical formula, that implies a value of one. Hence here we see a 2 preceding the H₂ in the reaction expression because two H₂ molecules participate as reactants in the hydrogen combustion reaction event. A plus sign then separates the chemical formula for H₂ from that for O₂, because O₂ also participates as a reactant in the hydrogen combustion reaction event. The absence of a number preceding the O₂ implies a value of 1, which is the number of O₂ molecules that participate in the reaction event as reactants. The numbers preceding the chemical species are called stoichiometric coefficients. The arrow in the reaction expression points to a similar listing of the chemical species that are products in the molecular reaction event.

A number of different styles of arrows are used when writing reaction expressions. The style of the arrow sometimes has special meaning. For example, sometimes a double arrow is used where there are two arrows one above the other and pointing in opposite directions (\(\rightleftarrows\)). A double arrow is a reminder that chemical reactions are bidirectional. It sometimes additionally signifies that the reaction is reversible, a concept that will be discussed later in this chapter.

Returning to the reaction expression for hydrogen combustion, a common way of reading a reaction expression is to read the reactants, say “goes to” and then read the products. Here, for example one could read the reaction expression as two H₂ plus one O₂ goes to two H₂O. Because chemical reaction events are bi-directional, the reaction as written in the reaction expression is sometimes called the forward reaction. For the reaction as written here, then, the reaction event where two water molecules react to form two hydrogen molecules and an oxygen molecule can be referred to as the reverse reaction.

Notice that the total number of each type of atom on the left side of the reaction expression is equal to the total number of that type of atom on the right side of the reaction expression. This is a consequence of reaction stoichiometry, and it must be true for every element that appears in a reaction expression. When it is true, the reaction expression is said to be balanced.

The reaction expression for hydrogen oxidation, above, is balanced because there are four H atoms on each side of the arrow and two O atoms on each side of the arrow. In that reaction expression, the number preceding each chemical formula is equal to the number of that species that participate in the molecular reaction event. This is not required, though. The reaction expression only needs to convey the proportions in which the reagents appear in the molecular reaction event, and not necessarily the exact number of molecules of the reagents.

\[ H_2 + \frac{1}{2} O_2 \rightarrow H_2O \tag{1.2}\]

Reaction 1.2 is an equally valid reaction expression for hydrogen combustion. Clearly, the stoichiometric coefficients here are not equal to the number of the molecules in the molecular reaction event, because there is no such thing as one-half of an O₂ molecule. Nevertheless, it is sometimes convenient to write the reaction expression so that the stoichiometric coefficient of one of the products has a magnitude of one. An example is the reaction expression used for a heat of formation (see Appendix D). It still is required that the reaction expression be balanced. In Reaction 1.2 there are 2 H atoms and 1 O atom on each side of the arrow, so it is balanced. Those are the same proportions as when the reaction expression is written as in Reaction 1.1.

As previously noted, the numbers that appear in a reaction expression, including the implied ones, are called stoichiometric coefficients. Each unique chemical species that participates in the molecular reaction event has a corresponding stoichiometric coefficient in the reaction expression. It is important to note that the stoichiometric coefficients are taken from the reaction expression, not the reaction event. In other words, the stoichiometric coefficient of H₂O in the hydrogen combustion reaction could be either one or two, depending upon which of the two reaction expressions, Reaction 1.1 or Reaction 1.2, is being used to represent the reaction event.

The lower-case Greek letter, \(\nu_{i,j}\), is used in Reaction Engineering Basics to represent stoichiometric coefficients. The first subscript, \(i\), identifies the chemical species, so \(i\) will be a chemical formula. If more than one reaction is taking place, there will be a second subscript, \(j\). The subscript \(j\) identifies one of the reactions taking place. Typically, when solving problems, we number the reactions, in which case \(j\) will be a number.

Reaction Engineering Basics uses a sign convention for stoichiometric coefficients where \(\nu\) for a species appearing as a reactant in the reaction expression is negative, and \(\nu\) for a species that is a product in the reaction expression is positive. (See Appendix C for a complete listing of sign conventions and notation used in Reaction Engineering Basics.) Thus, the stoichiometric coefficient of H₂ in Reaction 1.1 is written as \(\nu_{H_2,1.1}\) and is equal to -2. If a species does not appear in the reaction expression for reaction \(j\), then its stoichiometric coefficient in reaction \(j\) is equal to zero.

Again, it is very important to realize and remember that the magnitude of a species’ stoichiometric coefficient is the number that preceeds it in the reaction expression. That may or may not equal the number of molecules of that species participating in the molecular reaction event. As shown here, the stoichiometric coefficients of the reagents in hydrogen combustion change, depending upon the way the reaction expression is written.

1.1.3 Chemical Reaction Thermodynamics

Chemical reactions are processes where chemical bonds are formed and broken. Chemical bonds can be viewed as a form of stored energy. Chemical bond strength, that is, the amount of energy stored in chemical bonds, varies from bond type to bond type. As a consequence, when bonds break and form during a chemical reaction, there is a net change in the amount of energy being stored in chemical bonds. As a reaction takes place, that difference in the amount of stored energy between reactants and products is released into or extracted from the system in the form of heat. That heat is called the heat of reaction. If heat is extracted from the system, the heat of reaction is positive and the reaction is called an endothermic reaction. If heat is released into the system, the heat of reaction is negative and the reaction is called an exothermic reaction. Appendix D presents a brief review of how to calculate the heat of a given reaction.

All chemical reactions are bidirectional. When the rate at which reactants are being converted into products is equal to the rate at which products are being converted into reactants, the reaction is at equilibrium. At reaction equilibrium, the composition of the system is static; it does not change. Thermodynamics can be used to calculate an equilibrium constant, which, in turn can be used to calculate the composition of the system at reaction equilibrium. The equilibrium constant for a reaction changes with the system temperature. Appendix D presents a brief review of how to calculate equilibrium constants and the equilibrium composition for a reacting system.

1.1.4 Composition of Reacting Systems

The systems considered so far in this chapter contained only contain enough atoms for a chemical reaction to occur one time. Systems of that size are great for the purpose of defining a chemical reaction. There were basically only two possibilities for the components of those systems. Depending upon the bonding, the system either consisted of one set of reactant molecules or it consisted of one set of product molecules. When it comes to reaction engineering or any other real-world chemical process, however, the chemical systems that need to be considered contain on the order of Avodadro’s number (6.022 x 10²³) of molecules. Even if only one reaction is possible, that reaction can occur many, many times in any system of practical size. The individual molecular events do not all occur at the same time. As a consequence, the composition of the system changes over time, and means of characterizing the composition are needed.

Reaction Engineering Basics always assumes that gas phase systems are ideal. For a pure (single component) gas Equation 1.3 is the equation of state, and Equation 1.4 is the equation of state for gas mixtures.

\[ PV=nRT \tag{1.3}\]

\[ PV=RT\sum_i n_i \tag{1.4}\]

In Reaction Engineering Basics, liquids are incompressible and form ideal mixtures. As such, Equation 1.5 is the equation of state for a pure liquid and Equation 1.6 is the equation of state for a liquid mixture.

\[ \rho = \text{constant} \tag{1.5}\]

\[ \rho = \sum_i \left(\omega _i \rho _i\right) \tag{1.6}\]

Concentration, Equation 1.7, density, Equation 1.8, mole fraction, Equation 1.9, and mass fraction, Equation 1.10, are composition variables that can be used for either gas or liquid systems.

\[ C_i = \frac{n_i}{V} \tag{1.7}\]

\[ \rho = \frac{m}{V} \tag{1.8}\]

\[ x_i = \frac{n_i}{\displaystyle \sum _i\left(n_i\right)} \tag{1.9}\]

\[ \omega _i = \frac{m_i}{\displaystyle \sum _i \left(m_i\right)} \tag{1.10}\]

The density is related to the concentrations as shown in Equation 1.11.

\[ \rho = \sum _i \left( M_iC_i \right) \tag{1.11}\]

For gas phase systems, the partial pressure, Equation 1.12, is another composition variable.

\[ P_i = y_iP = \frac{n_iRT}{V} = C_iRT \tag{1.12}\]

In addition to being small, the chemical systems considered up to this point were closed systems. The discussion mentioned the reagents initially present in the system. Then it continued by discussing what was present in the system at later times. Chemical reactions also take place in open systems where reagents are continually entering the system as a feed stream and leaving it as a product stream. If a chemical reaction takes place in a steady-state flow system, the starting composition is the composition of the feed stream, and the ending composition is the composition of the product stream.

In closed systems, the moles of each of the species are natural variables to use to describe changes in composition. In an open, steady-state system, the composition changes between the entrance or inlet of the system and the outlet, but at any one point it is constant over time. In such a system, the molar flow rates of the species are natural variables to use to describe the changes. Reaction Engineering Basics uses variable symbols with dots over them to indicate flows. For example, \(n_i\), denotes the moles of reagent \(i\) while \(\dot n_i\) represents the molar flow rate of reagent \(i\). (See Appendix C for a complete listing of the notation used in Reaction Engineering Basics.) Thus, open systems are described using Equations 1.13 through 1.19 instead of Equations 1.3, 1.4, 1.7, 1.8, 1.9, 1.10, and 1.12.

\[ P\dot V=\dot nRT \tag{1.13}\]

\[ P\dot V=RT\sum_i \dot n_i \tag{1.14}\]

\[ C_i = \frac{\dot n_i}{\dot V} \tag{1.15}\]

\[ \rho = \frac{\dot m}{\dot V} \tag{1.16}\]

\[ x_i = \frac{\dot n_i}{\displaystyle \sum _i\left(\dot n_i\right)} \tag{1.17}\]

\[ \omega _i = \frac{\dot m_i}{\displaystyle \sum _i \left(\dot m_i\right)} \tag{1.18}\]

\[ P_i = y_iP = \frac{\dot n_iRT}{\dot V} = C_iRT \tag{1.19}\]

In large systems, it is quite possible that the numbers of molecules of each of the different reactants are not in stoichiometric proportion. If the forward reaction were to occur a sufficient number of times, one of the reactants would be completely used up while molecules of the other reactants still remained. The reactant that is completely used up is called the limiting reactant because the net number of times the forward reaction can occur is limited by the starting number of molecules of that reactant. The limiting reactant, or reactants if more than one would run out simultaneously, can be identified if you know the number of molecules or moles of each reactant that was present initially or in the feed. As shown in Equations 1.20 (for closed systems) and 1.21 (for open systems), the initial or starting number of moles of each reactant is divided by the magnitude of its stoichiometric coefficient. The resulting values might be referred to as the “stoichiometric equivalences” of the reactants. The reactant with the smallest stoichiometric equivalence is then the limiting reactant. If the resulting value is the same for all reactants, that means that the initial composition is a stoichiometric mixture and no reactant is limiting. If a reaction had 3 reactants with two having the same stoichiometric equivalence and the third having a greater value, then either or both of the reactants with the smaller value could be considered to be the limiting reactant.

\[ \frac{n_{lr,0}}{\left| \nu_{lr} \right|} < \frac{n_{nlr,0}}{\left| \nu_{nlr} \right|} \tag{1.20}\]

\[ \frac{\dot n_{lr,in}}{\left| \nu_{lr} \right|} < \frac{\dot n_{nlr,in}}{\left| \nu_{nlr} \right|} \tag{1.21}\]

Example 1.4.1 shows how to use the criterion presented here to identify the limiting reactant in a given reaction system.

1.1.5 Classifying Reactions

There are a number of different ways of characterizing reactions. A few have already been mentioned. One being classification based on the number of reactants participating in the molecular reaction event. That classification differentiates unimolecular, bimolecular, termolecular and intramolecular reactions. Another classification based upon the molecular reaction event is whether the reaction is elementary (all bonds break and form simultaneously) or non-elementary (the bonds break and form sequentially). From a macroscopic perspective a non-elementary reaction appears to be occurring, but at the molecular level, two or more molecular reaction events are actually taking place. The third is a thermodynamic classification based on the heat of reaction whereby reactions are classified as exothermic or endothemic.

Another thermodynamic classification is based upon the equilibrium composition for a reaction. All molecular reaction events are reversible. If you start with reactant molecules, they can convert to product molecules, and if you start with product molecules they can convert to reactant molecules. This is known as the principle of microscopic reversibility. As a consequence, in a large reacting system, there will always be some reactant molecules present because some of the product molecules will be reacting to re-generate reactant molecules. Eventually chemical reaction equilibrium is reached and the composition will become constant. If the amount of the limiting reactant that remains when the system reaches equilibrium is negligibly small, the reaction is said to be irreversible. In contrast, if the amount of the limiting reactant that remains when the system reaches equilibrium is appreciable, the reaction is said to be reversible. It was noted previously that double arrows (\(\rightleftarrows\)) in a chemical reaction expression may signify that the reaction is reversible.

Quite often, two or more chemical reactions take place at the same time in a chemical system. In these cases, additional classification of groups of reactions is sometimes possible. When a group of reactions all have the same reactants, but different products, that group is called a set of parallel reactions. The general form of parallel reactions is shown in Reactions 1.22. An example of parallel reactions is the chlorination of toluene, Reactions 1.23. Toluene and chlorine are the reactants in all of those reactions, but the products differ. The first reaction produces ortho-chlorotoluene, the second produces meta-chlorotoluene, and the third produces para-chlorotoluene.

\[ \begin{aligned} A \rightarrow Y \\ A \rightarrow Z \end{aligned} \tag{1.22}\]

\[ \begin{aligned} C_7H_8 + Cl_2 \rightarrow o-C_7H_7Cl + HCl \\ C_7H_8 + Cl_2 \rightarrow m-C_7H_7Cl + HCl \\ C_7H_8 + Cl_2 \rightarrow p-C_7H_7Cl + HCl \end{aligned} \tag{1.23}\]

Multiple reactions can also occur as series reactions. This means that the reactions occur sequentially, in the sense that the product of one reaction is the reactant in another reaction, as shown in Reactions 1.24, where D is the product of the first reaction and the reactant in the second reaction. In series reactions, the intermediate product, D in the case of Reactions 1.24, is often the more valuable, or desired, product, and the final product, U, is less valuable or undesired. An example of series reactions is the dehydrogenation of cyclohexane to benzene, Reactions 1.25. Cyclohexadiene is produced in the first reaction and reacts in the second reaction to yield cyclohexene. Then the cyclohexene reacts in the third reaction to produce benzene.

\[ \begin{aligned} A \rightarrow D \\ D \rightarrow U \end{aligned} \tag{1.24}\]

\[ \begin{aligned} C_6H_{12} \rightarrow C_6H_{10} + H_2 \\ C_6H_{10} \rightarrow C_6H_8 + H_2 \\ C_6H_8 \rightarrow C_6H_6 + H_2 \end{aligned} \tag{1.25}\]

A third kind of multiple reaction network involves series-parallel reactions. They are a kind of hybrid of series reactions and parallel reactions. From the perspective of one reactant, the group of reactions appear to be series reactions while from the perspective of the other reactant, it appears to be a parallel reaction network. Looking at the general example in Reactions 1.26, D is a product of the first reaction and it is a reactant in the second reaction. At the same time, B is a reactant in both reactions. So from the perspective of A being converted to D which is subsequently converted to U, it looks like a series reaction network but from B’s perspective it looks like a parallel reaction network. Reactions 1.27 is an example of a three-reaction series-parallel network. Methane is converted in parallel, while mono-methyl, di-methyl- and tri-methylamine are generated sequentially.

\[ \begin{aligned} A + B \rightarrow D + Y \\ D + B \rightarrow U + Z \end{aligned} \tag{1.26}\]

\[ \begin{aligned} NH_3 + CH_4 \rightarrow NH_2CH_3 + H_2 \\ NH_2CH_3 + CH_4 \rightarrow NH\left(CH_3\right)_2 + H_2 \\ NH\left(CH_3\right)_2 + CH_4 \rightarrow N\left(CH_3\right)_3 + H_2 \end{aligned} \tag{1.27}\]

Polymerization reactions are another type of multiple reaction network. Whole books and whole courses are devoted to polymerization reactions, so there’s lots more to it that what’s presented here. For present purposes, it can be noted that polymerization reactions share some of the characteristics of series-parallel reactions. In a simple example, Reactions 1.28, one reactant participates in parallel. It is called the monomer, and is represented here as M. The difference is that there may be thousands of sequential reactions. As a consequence, there are many, many products, differing in the number of monomer units they were made from. There isn’t one desired product, but often the goal is to produce predominantly products where the value of \(n\) falls in a certain range. Ethylene polymerization to produce polyethylene, Reaction 1.29, is an example of a polymerization reaction.

\[ \begin{aligned} M + M \rightarrow M_2 \\ M + M_2 \rightarrow M_3 \\ \vdots \\ M + M_{n-1} \rightarrow M_n \end{aligned} \tag{1.28}\]

\[ n C_2H_4 \rightarrow \; -\left(CH_2-CH_2\right)_n- \tag{1.29}\]

1.2 Chemical Reactors

Defining a chemical system involves identifying or specifying physical boundaries and describing chemical events that happen within those boundaries. In Reaction Engineering Basics the boundaries typically will encompass chemical process equipment, and chemical reactions will be among the events occurring within those boundaries. The term reactor often refers to a physical container, such as a flask, beaker, tank, pipe, etc., within which one or more chemical reactions occur. In that case, the physical walls of the reactor define the boundaries of the chemical system.

A reactor does not have to be a piece of apparatus, though. The human liver can be modeled as a chemical reactor . Neither does it have to possess physical walls. The earth’s atmosphere can be modeled as a chemical reactor. Many of the principles presented in this book can be used in the development of models for systems like the human liver (Mitchell and Mendes 2013) and the earth’s atmosphere(Yang, Lu, and Hu 2013). Nonetheless, the reactors considered in Reaction Engineering Basics will be physical containers in almost all cases. When biological reactions take place within them, the name chemostat or fermentor is sometimes used instead of “reactor.”

Two types of reactors are the primary focus of Reaction Engineering Basics. One is a vessel wherein the contents are perfectly mixed. These are commonly referred to as stirred tank reactors. Stirred tank reactors may be open (that is have material flowing in and/or out) or they may be closed with no material flow in or out. The other type of reactor is a cylindrical tube within which the fluid velocity is constant across the tube diameter. Flow of that type is commonly called plug flow, and the reactors are called plug flow reactors.

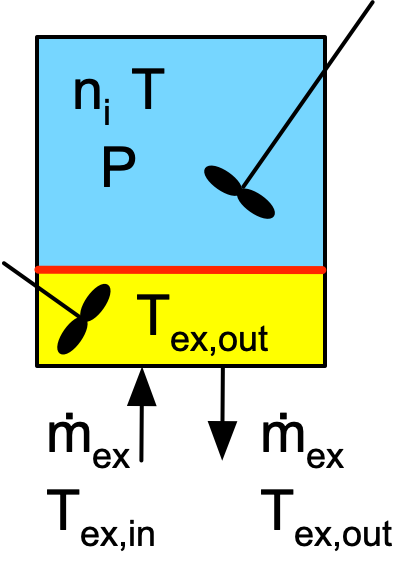
Reaction Engineering Basics examines ideal stirred tank reactors. The most important feature of ideal stirred tank reactors is that the contents are perfectly mixed at all times. If the contents of an ideal stirred tank reactor are sampled simutaneously at multiple locations within the stirred tank, the temperature, pressure and composition of every sample will be the same. Figure 1.3 presents a schematic representation of a closed stirred tank reactor that exchanges heat with an external heat exchange fluid. Chapter 6 describes three variants of stirred tank reactors (batch, semi-batch and continuous) and Appendix H derives equations used to model them. The volume containing the reacting fluid and the volume containing the heat exchange fluid are separated by a wall through which the fluids exchange heat. In Reaction Engineering Basics the heat exchange fluid is always assumed to be perfectly mixed, and the heat exchange fluid is assumed to exchange either sensible heat or latent heat, but not both. Appendix E describes heat exchange with stirred tanks in a little more detail and also presents equations used to model it.

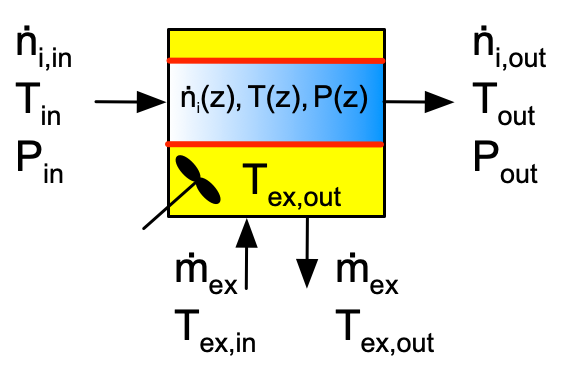
Figure 1.3: A closed (batch) stirred tank reactor. The reacting fluid is represented by the turquoise shading and the heat exchange fluid by yellow shading. The wall through which heat is exchanged is shaded red.

The ideal tubular reactors considered in Reaction Engineering Basics are always assumed to be cylindrical with a constant diameter. The fluid in an ideal tubular reactor is assumed to display plug flow. Figure 1.4 shows a schematic representation of a tubular reactor with heat exchange. Unlike stirred tanks, the temperature, pressure and composition change along the length of a plug-flow reactor. The same assumptions about perfect mixing of the heat exchange fluid and exchange of either sensible heat or latent* heat by that fluid are used. The wall through which heat is exchanged is always the wall of the tubular reactor. Equations for modeling plug-flow reactors are derived in Appendix H, and equations for modeling tubular reactor heat exchange are presented in Appendix E.

Figure 1.4: A plug-flow reactor. The reacting fluid is represented by blue shading. The gradient in the shading indicates that the temperature, pressure and composition change along the length of the cylindrical reactor. Heat can be exchanged through the wall of the reactor which is shaded in red. The perfectly mixed heat exchange fluid is represented by yellow shading.

Chemical processes, and, by extension, chemical reactors, can be classified in a few ways. One form of classification is based upon whether the reactor exchanges heat with its surroundings. If no energy is added to or removed from the reactor other that that associated with input and output flow streams, the reactor is said to be adiabatic. If energy is added or removed, the process is non-adiabatic.

Another form of classification is based upon variables describing the process being constant. If the temperature is uniform (the same everywhere) throughout the reactor and constant while the process occurs, the process is said to be isothermal. Similarly, if the pressure throughout the reactor is uniform and constant while the process occurs, the reactor is said to be isobaric. A process is isochoric if the system volume is constant while the process occurs.

A third form of classification is based upon temporal (time) variations. If, at each location within the reactor, the temperature, pressure and composition are constant over time, the reactor is said to operate at steady-state. In a steady-state reactor, the temperature, pressure and composition may vary from location to location within the reactor, but at each location they are constant over time. If the temperature, pressure or composition vary over time at any location with a reactor, then it is called transient operation.

1.3 Reaction Engineering

Reaction engineering is an important, exciting and engaging field of study. It is important because it is used to produce many, many things we use every day (fuels, pharmaceuticals, cosmetics, processed foods, plastics, computer chips, etc.). It is exciting because it is expected to play a major role in meeting several of the grand challenges facing mankind (“NAE GRAND CHALLENGES FOR ENGINEERING” 2017). Specifically, there is a role for reaction engineering in making solar energy economical, developing carbon sequestration methods, managing the nitrogen cycle, providing access to clean water, and perhaps also in some aspects of providing energy from fusion, engineering better medicines, and engineering the tools of scientific discovery. It is not only engaging because reaction engineers can work to solve important, meaningful problems, but also because practitioners can be highly creative when solving reaction engineering problems.

Chemical reaction engineering is a sub-discipline of chemical engineering that focuses upon processes involving one or more chemical reactions. It incorporates the modeling, optimization, design and operation of chemical reactors. That modeling involves the integration of fluid flow, mass and heat transfer and chemical reaction kinetics to mathematically describe reactor systems.

Reaction engineering models allow reaction engineers and others to understand reaction processes and predict their behavior before investing time and money in building them. The models reveal necessary equipment size, energy requirements, wastes that are co-produced, and so on. Using them, the procedures for safely starting, operating and shutting down processes can be specified. The models can also be used to calculate the economics of building and operating processes.

Reaction engineers must be creative and need skills beyond building models. They must be able to create new processes and adapt existing processes to make new products while satisfying safety, environmental and economic constraints. Reaction engineers must be able to locate or generate data required by their models and they need the ability to validate and revise their models using experimental data. Reaction engineers must function effectively as members of multidisciplinary teams that include experts in business, finance, health, safety, environmental and regulatory compliance, logistics, operations, chemistry and others.

Reaction Engineering Basics offers an introduction to reaction engineering. While it is limited in scope, it illustrates many of the kinds of problems that reaction engineers encounter. Chemical kinetics is a sub-discipline of chemistry that focuses upon the rates of chemical reactions. Reaction Engineering Basics introduces essential aspects of chemical kinetics, in particular, the generation and analysis of data for the purpose of generating rate expressions for chemical reactions. Appendix B presents an overview of knowledge that readers of Reaction Engineering Basics are expected to possess. Solving reaction engineering models requires knowledge from the field of mathematics. Reaction Engineering Basics assumes model equations will be solved numerically. Appendices I through K present an overview of numerical methods that are commonly used to solve reaction engineering model equations.

1.4 Example

1.4.1 Identifying the Limiting Reactant

Carbon monoxide can be oxidized by molecular oxygen to produce carbon dioxide as shown in reaction (1). If equal volumes of carbon monoxide and air at equal temperature and pressure are mixed and flow into a chemical reactor, which reactant is limiting?

\[ 2 CO + O_2 \rightarrow 2 CO_2 \tag{1} \]

Click Here to see What Might an Expert be Thinking at this Point

The problem asks me to identify the limiting reactant, and that means that I will need to use either Equation 1.20 or Equation 1.21. It also states that CO and air flow into the reactor. That means it is an open reactor, and Equation 1.21 should be used to identify the limiting reactant. The reactants and their stoichiometric coefficients can be determined from the balanced chemical reaction which is given as reaction (1).

Limiting Reactant Criterion

\[ \frac{\dot n_{lr,in}}{\left| \nu_{lr} \right|} < \frac{\dot n_{nlr,in}}{\left| \nu_{nlr} \right|} \tag{2} \]

Reactants: CO and O₂

Stoichiometric Coefficients of the Reactants: \(\nu_{CO} = -2\) and \(\nu_{O_2} = -1\)

Click Here to see What an Expert Might be Thinking at this Point

The problem does not give me enough information to calculate the inlet molar flow rates. However, since it doesn’t give any extensive quantities, I can assume the inlet volumetric flow rate of CO or air as a basis. (According to the problem statement they are equal.) I still can’t calculate the inlet molar flow rates, though, because I don’t know the temperature or pressure. However, I do know that the gases are ideal, so I can try re-writing equation (2) in terms of volumetric flow rates.

Using the ideal gas law the molar flow rates in equation (2) can be expressed in terms of the volumetric flow rates.

\[ \frac{P\dot V_{lr,in}}{RT\left| \nu_{lr} \right|}< \frac{P\dot V_{nlr,in}}{RT\left| \nu_{nlr} \right|} \]

Multiplying both sides by \(\frac{RT}{P}\) yields a limiting reactant criterion in terms of inlet volumetric flow rates, equation (3).

\[ \frac{\dot V_{lr,in}}{\left| \nu_{lr} \right|} < \frac{\dot V_{nlr,in}}{\left| \nu_{nlr} \right|} \tag{3} \]

Basis: \(\dot V_{CO,in}\) = 1 L s^-1.

According to the problem statement the inlet volumetric flow rates of air and CO are equal, so \(\dot V_{\text{air},in}\) = 1 L s^-1.

Assuming that air is 21% O₂ and 79% other non-reactive gases (predominantly N₂) allows calculation of the inlet volumetric flow rate of O₂, equation (4). At that point the stoichiometric equivalences of CO and O₂ can be calculated, equations (5) and (6).

\[ \dot V_{O_2,in} = 0.21 \dot V_{\text{air},in} = 0.21 \text{ L s}^{-1} \tag{4} \]

\[ \frac{\dot V_{CO,in}}{\left| \nu_{CO} \right|} = \frac{1 \text{ L s}^{-1}}{\left|-2\right|} = 0.5 \text{ L s}^{-1} \tag{5} \]

\[ \frac{\dot V_{O_2,in}}{\left| \nu_{O_2} \right|} = \frac{0.21 \text{ L s}^{-1}}{\left|-1\right|} = 0.21 \text{ L s}^{-1} \tag{6} \]

The stoichiometric equivalence of O₂ is smaller than that of CO, so O₂ is the limiting reactant.

Note

There are other ways to solve this problem. In the solution presented here, the volumetric flow rate of CO was chosen as a basis for the calculations. An alternative approach would be to choose the molar flow rate of air or CO as a basis. Doing so is left as an exercise for the reader.

1.5 Symbols Used in Chapter 1

Symbol	Meaning
\(i\)	Subscript denoting a fluid phase reagent.
\(j\)	Subscript denoting a reaction occurring in the system.
\(lr\)	Subscript denoting a limiting reactant.
\(m\)	Mass; a subscripted \(i\) denotes the mass of reagent \(i\)
\(\dot m\)	Mass flow rate; a subscripted \(i\) denotes the mass flow rate of reagent \(i\).
\(n\)	Number of moles; a subscripted \(i\) denotes the number of moles of reagent \(i\); an additional subscripted \(0\) denotes the initial moles.
\(\dot n\)	Molar flow rate; a subscripted \(i\) denotes the molar flow rate of reagent \(i\); an additional subscripted \(in\) denotes the inlet molar flow rate.
\(nlr\)	Subscript denoting a reactant that is not a limiting reactant.
\(x_i\), \(y_i\)	Mole fraction of reagent \(i\); \(x_i\) is commonly used for liquid phase mole fractions and \(y_i\) for gas phase mole fractions.
\(C_i\)	Molar concentration of reagent \(i\).
\(M_i\)	Molecular weight of reagent \(i\).
\(P\)	Pressure; a subscripted \(i\) denotes the partial pressure of reagent \(i\).
\(R\)	Ideal gas constant.
\(T\)	Temperature.
\(V\)	Volume.
\(\dot V\)	Volumetric flow rate; a subscripted \(i\) denotes the volumetric flow rate of reagent \(i\).
\(\nu_{i,j}\)	Stoichiometric coefficient of reagent \(i\) in reaction \(j\); if only one reaction is taking place the index, \(j\) is optional.
\(\rho\)	Density; a subscripted \(i\) denotes the density of reagent \(i\).
\(\omega _i\)	Mass fraction of reagent \(i\).