15 Reactor Networks
This chapter considers systems wherein two or more reactors are connected in some way and function together in the processing of a single feed stream. Reasons for using more than one reactor are discussed, and the qualitative and quantitative analyses of reactor networks are presented.
15.1 Reactor Networks
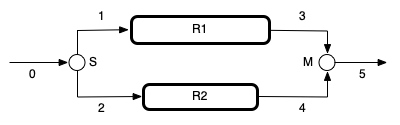
In the preceding chapters, isolated reactors were considered. A chemical process can use more than one reactor to process a feed stream. The most common configurations of multiple reactors are series networks of reactors and parallel networks of reactors, as illustrated in Figure 15.1. Panel (a) of that figure shows two CSTRs in series where the reactors are labeled R1 and R2. Series networks are not limited to two reactors; there can be any number of reactors as long as the outlet from each one becomes the feed to the next. Series networks of PFRs are equally possible.
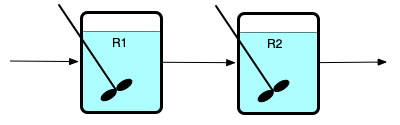

The (b) panel of Figure 15.1 shows two PFRs, labeled R1 and R2, that are connected to form a parallel network. Again, there can be any number of reactors in a parallel network, as long as a single stream is split, and distributed among the reactors, and as long as the outlet streams from all of the reactors are mixed into a single product stream. In the figure, S is used to denote a stream splitter and M is used to denote a stream mixer. Parallel networks can also be created using CSTRs.
Another possibility with series or parallel reactor networks is that the reactors might not be of the same type. For example an engineer could design a CSTR in series with a PFR with either of the two reactors first in the series network. Similarly, a CSTR in parallel with a PFR is also possible.
Reactor networks that are neither series nor parallel are also possible. Such networks are not common in commercial processing. However, Chapter 25 shows how reactor networks can be used to model a single, non-ideal reactor. In that situation, the reactor network need not be a series or parallel network.
15.2 Analysis of Reactor Networks
15.2.1 Qualitative Behavior of Reactor Networks
A series network of adiabatic PFRs is equivalent to a single adiabatic PFR with a volume equal to the total volume of the series PFRs. If the individual PFRs are heated or cooled, or if there is heating or cooling between one PFR outlet and the next PFR inlet, the performance of the network will be different from a single PFR with the same total volume.
In a parallel network of equally-sized PFRs where the feed is evenly split among the reactors, the temperature and concentration profiles along the length of each reactor are the same as for the other reactors. This assumes that the PFRs are either adiabatic, or they all pass through a single shell within which a perfectly mixed exchange fluid flows. It won’t be true if the heat exchange is different in different reactors.
A series network of isothermal or adiabatic CSTRs becomes equivalent to a single PFR with the same total volume as the number of CSTRs approaches infinity. A series network of CSTRs is sometimes referred to as a CSTR cascade. Figure 13.2 showed that because there is no mixing in the axial direction in a PFR, the fluid can be envisioned as small batch reactors that enter the reactor one after the other, with each batch reactor moving from the inlet to the outlet at a velocity equal to the velocity of the fluid flowing in the PFR. Another way to think of this is that the little BSTRs are stationary CSTRs, and the fluid moves from one to the next. Since each CSTR is differentially small, it is easy to understand why an infinite series of CSTRs is equivalent to a PFR.
If each of the CSTRs in a series network are heated or cooled by exchange of heat with a perfectly mixed exchange fluid, the series will not approach the bahavior of a PFR as the number of CSTRs approaches infinity.
In a parallel network of equally sized and equally cooled/heated CSTRs, if the feed is divided equally among the reactors, the contents of every reactor will be the same.
Finally, if parallel reactors are used, the mixing streams of unequal conversion should be avoided. Doing so effectively undoes some of the reaction that has taken place because after mixing the effective conversion of the mixed stream will be lower than that in the stream with the higher conversion before mixing.
15.2.2 Quantitative Analysis of Reactor Networks
It is good practice to label each flow stream in the process and each piece of equipment. Variables representing flow rates, temperatures, pressures, etc. can then be subscripted using the labels to denote the stream or equipment to which the variable applies. Here, only steady-state operation will be considered. The only equipment that may be present in the networks considered here are stream splitters, stream mixers, and heat exchangers. Quantitative analysis of a reactor network requires writing the reactor design equations for each reactor in the network and writing mole and energy balances for every splitter, mixer and heat eachanger in the network.
The analysis of any one of the reactors in a network is no different from the analysis of an isolated reactor. After all, it makes no difference in the analysis of a reactor whether the feed to that reactor is coming from a storage tank somewhere in the chemical plant or from the outlet of another reactor. Similarly, it makes no difference in the reactor analysis whether the product stream is sent to a distillation tower elsewhere in the chemical plant or to another reactor. Thus, the reactor design equations for each reactor are generated as described in Chapter 6 and illustrated in Chapters 12 and 13.
A stream splitter will have one inlet stream and two or more outlet streams. A steady-state mole balance on reagent \(i\) takes the form shown in Equation 15.1 where \(N_{out}\) denotes the number of outlet streams and “out” indexes those streams. It is important to recognize that the temperatures of all entering and leaving streams are equal. As such, instead of writing energy balances, the temperatures of each of the streams leaving the splitter can simply be set equal to the temperature of the stream entering the splitter, Equation 15.2. Similarly, a splitter does not change concentration (or partial pressure); the concentration (or partial pressure) of reagent \(i\) in every outlet flow stream is equal to its concentration (or partial pressure) in the input stream.
\[ 0 = \dot{n}_{i,in} - \sum_{N_{out}} \dot{n}_{i,out} \tag{15.1}\]
\[ T_{out} = T_{in} \text{ ; } \quad out = 1...N_{out} \tag{15.2}\]
A stream mixer will have two or more inlet streams and one outlet stream. A steady-state mole balance on reagent \(i\) takes the form shown in Equation 15.3 where \(N_{in}\) denotes the number of outlet streams and “in” indexes those streams. An energy balance takes the form shown in Equation 15.4. In both equations, \(\displaystyle \sum_{in}\) denotes a summation of all of the inlet streams. For liquid flow streams, equivalent energy balances can be written in terms of the volumetric heat capacity or the gravimetric heat capacity, Equation 15.5 and Equation 15.6.
\[ 0 = \dot{n}_{i,out} - \sum_{N_{in}} \dot{n}_{i,in} \tag{15.3}\]
\[ 0 = \sum_i \sum_{in} \left(\dot{n}_{i,in} \int_{T_{in}}^{T_{out}} \hat{C}_{p,i} dT \right) \tag{15.4}\]
\[ 0 = \sum_{in} \left(\dot{V}_{in} \int_{T_{in}}^{T_{out}} \breve{C}_p dT \right) \tag{15.5}\]
\[ 0 = \sum_{in} \left(\rho \dot{V}_{in} \int_{T_{in}}^{T_{out}} \tilde{C}_p dT \right) \tag{15.6}\]
Entire books and courses are devoted to heat transfer processes, and there are numerous variations in the design of heat exchangers. The discussion here will be limited to a simple heat exchanger, with two streams that do not mix flowing through it in opposite directions (counter-current flow). Denoting the streams as 1 and 2, mole balances take the form shown in Equations 15.7 and 15.8. The energy balance, Equation 15.9, assumes no heat loss, and simply requires that the rate at heat is added to stream “1” must equal the rate at which heat is removed from stream “2.” Those heats can be expressed in terms of molar heat capacities, volumetric heat capacities, or gravimetric heat capacities, Equations 15.10, 15.11, and 15.12.
\[ 0 = \dot{n}_{i,1,in} - \dot{n}_{i,1,out} \tag{15.7}\]
\[ 0 = \dot{n}_{i,2,in} - \dot{n}_{i,2,out} \tag{15.8}\]
\[ 0 = \dot{Q}_{1} - \dot{Q}_{2} \tag{15.9}\]
\[ \dot{Q}_{x} = \sum_i \left( \dot{n}_{i,x,in} \int_{T_{x,in}}^{T_{x,out}}\hat{C}_{p,i} dT\right); \qquad x = 1 \text{ or } 2 \tag{15.10}\]
\[ \dot{Q}_{x} = \dot{V}_{x,in} \int_{T_{x,in}}^{T_{x,out}} \breve{C}_{p,x} dT; \qquad x = 1 \text{ or } 2 \tag{15.11}\]
\[ \dot{Q}_{x} = \rho_{x} \dot{V}_{x,in} \int_{T_{x,in}}^{T_{x,out}} \tilde{C}_{p,x} dT; \qquad x = 1 \text{ or } 2 \tag{15.12}\]
If the temperatures of only two of the four streams are known, an additional equation for the rate of heat transfer may be needed. The physical design and dimensions of the heat exchanger and the properties of the fluids determine how much heat is transferred from stream 1 to stream 2. A common way to express this mathematically is in the form of expressions for the rate of heat transfer like Equation 15.13 or Equation 15.14. The log-mean and arithmetic mean temperature differences appeaing in those equations are defined in Equation 15.15 and Equation 15.16. The log-mean temperature diference becomes indeterminate if \(\left(T_{1,in} - T_{2,out}\right) = \left( T_{1,out} - T_{2,in} \right)\). In this situation it should be taken to equal either \(\left(T_{1,in} - T_{2,out}\right) or \left( T_{1,out} - T_{2,in} \right)\).
\[ \dot{Q}_{x} = U_{LM}A \Delta T_{LM}; \qquad x = 1 \text{ or } 2 \tag{15.13}\]
\[ \dot{Q}_{x} = U_{AM}A \Delta T_{AM}; \qquad x = 1 \text{ or } 2 \tag{15.14}\]
\[ \Delta T_{LM} = \frac{\left(T_{1,in} - T_{2,out}\right) - \left( T_{1,out} - T_{2,in} \right)}{\ln{\displaystyle\frac{T_{1,in} - T_{2,out}}{T_{1,out} - T_{2,in} }}} \tag{15.15}\]
\[ \Delta T_{AM} = \frac{\left(T_{1,in} - T_{2,out}\right) + \left(T_{1,out} - T_{2,in}\right)}{2} \tag{15.16}\]
Once reactor design equations have been written for every reactor and for each heat exchanger, stream splitter and stream mixer, those equations need to be solved. The manner in which this is accomplished will depend upon the specific network being analyzed and the information that is known about that network. In some situations, it may be possible to solve the reactor design equations for the reactors and the mole and energy balances for the other equipment sequentially. In other situations the reactor design equations for one reactor may be coupled with the reactor design equations for another reactor or with the mole and energy balances for one or more of the other pieces of equipment. In thise cases, the coupled equations must be solved simultaneously.
In other words, there isn’t a single “recipe” for solving the model equations. Once all of the equations have been formulated, they can be inspected to determine whether any of them can be solved independently of the others. If so, that can be done, after which it will be necessary to devise a strategy for solving the remaining equations.
15.3 Reasons for Using a Reactor Network
There are different reasons why a reactor network might be used instead of a single reactor. One possibility is expanding the capacity of an existing chemical plant. If a company decides to substantially increase the amount of material they are processing, the existing reactor may not be able to accommodate the increase. Increasing the flow rate to process more reactant will lower the residence time, and that generally will lower the conversion, offsetting the increased flow. It may make sense to continue using the existing reactor and add a second reactor to the process rather than eliminating the existing reactor and replacing it with a single, larger reactor.
In other cases, multiple reactors might be part of the original design. An example is the use of PFRs where it is necessary to heat or cool. It is quite common to use a large number of reactor tubes arranged in parallel, with a single shell surrounding all the tubes to provide heat transfer.
As described in Chapter 14, when a single CSTR is used, the reaction takes place at the final composition and temperature. When a single PFR is used, the composition and temperature vary continuously from their inlet values to their outlet values. Another reason for using multiple reactors is to change the temperature vs. reaction time or composition vs. reaction time. As an example, if two PFRs in series are used, each with cooling by heat exchange with a perfectly mixed heat exchange fluid, the temperature vs. reaction time will be different from that of a single PFR using the same exchange fluid. Sometimes it is possible to design a reactor network where the temperature vs. reaction time and/or composition vs. reaction time results in better performance than a single reactor. That is, a reactor network may require a smaller total reactor volume or it may offer better selectivity than a single reactor.
Consider the difference between a single isothermal CSTR and two isothermal CSTRs in series. The single CSTR will operate at the final composition. For most reactions, this means that the rate will be small due to low concentration of reactant. When two CSTRs in series are used to convert an equal amount of reactant, the second CSTR will operate at the same final composition where the rate is low. However, the first CSTR will operate at a higher concentration of reactant and a correspondingly higher rate. Because part of the conversion is taking place at a higher rate, the total volume that is required will be smaller than a single CSTR where the rate is always low.
If the reaction is exothermic and the reactor operates adiabatically, then the increase in temperature (and its tendency to increase the rate) often will predominate over the decrease in reactant concentration (and its tendency to decrease the rate). A simple qualitative analysis will show that there will be a critical conversion, and a corresponding critical space time, where the rate reaches a maximum. If one were judicious in selecting the relative volumes of the two reactors in series, the first could be designed so that it operated at the critical space time where the reaction rate was at its maximum value. Then the second CSTR in series would be sized so that the desired overall conversion is achieved.
There are also situations where it might make sense to use two different kinds of reactor in a network. For example, consider an autocatalytic reaction such as cell growth. If one wanted to use a plug flow reactor for cell growth, the feed stream would always need to contain cells and substrate. However, if a small CSTR was installed in series ahead of the PFR, only substrate would need to be supplied in the feed. As long as cells are growing in the CSTR, the substrate would mix with those growing cells, and the feed to the PFR would contain both cells and substrate.
15.4 Examples
This chapter presents four examples of the analysis of simple reactor networks. The first three involve reactors in series while the last examines reactors in parallel. Example 15.4.1 compares series networks that include both a CSTR and a PFR, looking at the effect of which reactor is first. Example 15.4.2 illustrates a common situation where two packed bed reactors in series are used. Example 15.4.3 is an optimization problem where the feed and conversion are fixed for two CSTRs in series, and the assignment is to minimize the total volume. The last example tests the statement from this chapter that said mixing streams of unequal conversion should be avoided.
15.4.1 Comparing a CSTR Followed by a PFR to a PFR Followed by a CSTR
A 350 L adiabatic CSTR and a 350 L adiabatic PFR are going to be connected in series and used to convert reagent A according to irreversible reactions (1) and (2), where D is the desired product and U is an undesired, low-value byproduct. The feed consists of an aqueous stream containing 2.5 mol A L-1, flowing at a rate of 100 L min-1 at 38 °C. The liquid density may be assumed to be constant. The heat of reaction (1) is -21,500 cal mol-1 and that of reaction (2) is -24,000 cal mol-1. The heat capacity of the solution is constant and equal to 1.0 cal cm-3 K-1. The rate expressions for reactions (1) and (2) are given in equations (3), and (4), respectively. The pre-exponential factor for reaction (3) is 1.2 x 105 min-1, and the activation energy is 9100 cal mol-1. The Arrhenius parameters for reaction (4) are 2.17 x 107 L mol-1 min-1 and 13,400 cal mol-1. Compare the overall conversion of A and selectivity (mol D per mol U) for the configuration with the CSTR first to those with the PFR first.
\[ A \rightarrow D \tag{1} \] \[ A \rightarrow U \tag{2} \]
\[ r_1 = k_1 C_A \tag{3} \]
\[ r_1 = k_1 C_A^2 \tag{4} \]
This assignment involves a network of two reactors in series. Before summarizing the assignment, I will make a simple schematic where I label the reactors and the flow streams. I’ll use “R” with a number to denote the reactors and I’ll simply number the streams. Then I can use the labels as I summarize the assignment.
15.4.1.1 Assignment Summary
Network Schematic
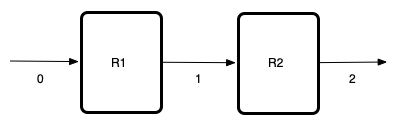
Given and Known Constants: \(V_{CSTR}\) = 350 L, \(V_{PFR}\) = 350 L, \(C_{A,0}\) = 2.5 mol L-1, \(\dot{V}_0\) = 100 L min-1, \(T_0\) = 38 °C, \(\Delta H_1\) = –21,500 cal mol-1, \(\Delta H_2\) = –24,000 cal mol-1, \(\breve{C}_p\) = 1.0 cal cm-3 K-1, \(k_{0,1}\) = 1.2 x 105 min-1, \(E_1\) = 9100 cal mol-1, \(k_{0,2}\) = 2.17 x 107 L mol-1 min-1, \(E_2\) = 13400 cal mol-1.
Reactor Systems: (a) adiabatic CSTR (R1) followed in series by an adiabatic PFR (R2), and (b) adiabatic PFR (R1) followed in series by an adiabatic CSTR (R2)
Quantities of Interest: \(f_A\) and \(S_{D/U}\)
15.4.1.2 Mathematical Formulation of the Solution
I know I need to generate the reactor design equations for each of the reactors. There isn’t any other equipment in this network, so no other mole and energy balances are needed.
The same reactor design equations will describe the CSTR irrespective of whether it is R1 or R2. However, the identy of the inlet and outlet streams will be different. To avoid writing two sets of CSTR design equations, I will use “in” to denote the stream flowing into the CSTR and “out” to denote the stream flowing out of the CSTR. Then, as I formulate the solution, I can set “in” equal to stream 0 for case (a), and I can set it equal to stream 1 for case (b).
Both reactors are adiabatic, so I need mole balances and an energy balance for each reactor. There is no mention of pressure drop in the PFR, and I don’t have sufficient information to calculate it, so I will assume negligible pressure drop in the PFR.
The general form of the steady-state CSTR mole balance is given in Equation 6.31. Here there are two reactions, so the summation expands to two terms.
\[ 0 = \dot{n}_{i,in} - \dot{n}_i + V \sum_j \nu_{i,j}r_j \Rightarrow \dot{n}_{i,in} - \dot{n}_{i,out} + V \left( \nu_{i,1}r_1 + \nu_{i,2}r_2\right) \]
The general form of the steady-state CSTR energy balance is given in equation Equation 6.32. In this system both the rate of heat transfer and the work are equal to zero, and the sensible heat term can be expressed in terms of the volumetric heat capacity given in the assignment narrative. At the same time, the constant heat capacity can be taken outside of the integral which can then be evaluated. As above, the summation over the reactions expands to two terms.
\[ \begin{align} 0 &= \cancelto{0}{\dot{Q}} - \cancelto{0}{\dot{W}} - \cancelto{\dot{V}_{in} \breve{C}_p \left( T_{out} - T_{in} \right)}{\sum_i\dot{n}_{i,in} \int_{T_{in}}^T \hat{C}_{p,i}dT} \\&- \cancelto{V \left( r_1 \Delta H_1 + r_2 \Delta H_2 \right)}{V\sum_j r_j \Delta H_j} \end{align} \]
The general form of the steady-state PFR mole balance is given in Equation 6.39. Noting that \(dV = \frac{\pi D^2}{4}dz\), the equation can be rewritten using the volume as the independent variable. Again, there are two reactions, so the summation expands to two terms.
\[ \frac{d \dot{n}_i}{d z} =\frac{\pi D^2}{4}\sum_j \nu_{i,j}r_j \quad \Rightarrow \quad \frac{d \dot{n}_i}{dV} = \nu_{i,1}r_1 + \nu_{i,2}r_2 \]
The general form of the steady-state PFR energy balance is given in Equation 6.40. The energy balance can also be rewritten using the volume as the independent variable. The reactor is adiabatic so the heat transfer term goes to zero. The sensible heat can be written in terms of the volumetric heat capacity, and the summation over the two reactions can be expanded.
\[ \cancelto{\dot{V} \breve{C}_p}{\left(\sum_i \dot{n}_i \hat{C}_{p,i} \right)} \frac{d T}{d z} = \cancelto{0}{\pi D U\left( T_{ex} - T \right)} - \frac{\pi D^2}{4}\sum_j r_j \Delta H_j \]
\[ \frac{d T}{dV} = -\frac{r_1 \Delta H_1 + r_2 \Delta H_2}{\dot{V} \breve{C}_p} \]
This is a liquid-phase system, so the volumetric flow rates of the three streams are all equal to \(\dot{V}_0\).
Reactor Design Equations
Steady-state mole balance design equations for A, D, and U in the CSTR are presented in equations (5), (6), and (7). The steady-state CSTR energy balance on the reacting fluid is given in equation (8). Steady-state mole and energy balances for the PFR are presented in equations (9) through (12).
\[ 0 = \dot{n}_{A,in} - \dot{n}_{A,out} + \left( -r_1 - r_2 \right)V_{CSTR} = \epsilon_1 \tag{5} \]
\[ 0 = \dot{n}_{D,in} - \dot{n}_{D,out} + r_1V_{CSTR} = \epsilon_2 \tag{6} \]
\[ 0 = \dot{n}_{U,in} - \dot{n}_{U,out} + r_2 V_{CSTR} = \epsilon_3 \tag{7} \]
\[ 0 = - \dot{V}_0 \breve{C}_p \left( T_{out} - T_{in} \right) - V_{CSTR} \left( r_1 \Delta H_1 + r_2 \Delta H_2 \right) = \epsilon_4 \tag{8} \]
\[ \frac{d \dot{n}_A}{dV} = -r_1 - r_2 \tag{9} \]
\[ \frac{d \dot{n}_D}{dV} = r_1 \tag{10} \]
\[ \frac{d \dot{n}_U}{dV} = r_2 \tag{11} \]
\[ \frac{d T}{dV} = -\frac{r_1 \Delta H_1 + r_2 \Delta H_2}{\dot{V}_0 \breve{C}_p} \tag{12} \]
The number of dependent variables in the PFR design equations, four, is equal to the number of IVODEs, so it isn’t necessary to eliminate a dependent variable or add an IVODE. I do need initial values and a stopping criterion, however.
I can define \(V_{PFR} = 0\) to be the PFR inlet. In that case, the initial values are simply the molar flow rates and the temperature at that point. For case (a) they are the values for stream 1 and for case (b) they are the values for stream 0. Stream 0 only contains A, so the flow rates of D and U are zero. In both cases, I know the total volume of the PFR and can use that as the stopping criterion.
Initial Values and Stopping Criterion
| Variable | Initial Value for Case (a) | Initial Value for Case (b) | Stopping Criterion |
|---|---|---|---|
| \(V\) | \(0\) | \(0\) | \(V_{PFR}\) |
| \(\dot{n}_A\) | \(\dot{n}_{A,1}\) | \(\dot{n}_{A,0}\) | |
| \(\dot{n}_D\) | \(\dot{n}_{D,1}\) | \(0\) | |
| \(\dot{n}_U\) | \(\dot{n}_{U,1}\) | \(0\) | |
| \(T\) | \(T_1\) | \(T_0\) |
Starting with case (a) where the CSTR is first, I will need to set the variables in equations (5) through (8) that are labeled “in” equal to the values for stream 0. That will leave the variables labeled “out”, \(r_1\), and \(r_2\) as unknown. I can solve the four CSTR design equations for the four variables labeled “out.” In order to do so, I’ll need to provide an initial guess for the variables labeled “out,” and I’ll need to evaluate the residuals each time a new guess for the solution is generated. At that point, I will have values for every quantity in the residuals expressions, equations (5) through (8) except \(r_1\) and \(r_2\).
The rates can be calculated using the rate expressions provided as equations (3) and (4). Before I can use them, I’ll need to calculate \(k_1\) and \(k_2\). I can do that using the Arrhenius expression, Equation 4.8. I’ll also need to calculate the concentration of A to substitute in the rate expression. I can use the defining equation for concentration in an open system, Equation 2.15 to do that, remembering that the rate is evaluated at the outlet composition and temperature.
After I solve the CSTR design equations, I can solve the PFR design equations for case (a). The PFR design equations are IVODEs, so I’ll need to do two things: calculate the values of the derivatives at the start of each integration step and calculate all of the initial and final values in Table 15.1. Having solved the CSTR design equations and set stream 1 equal to the CSTR outlet stream, all of the initial and final values will be known.
At the start of each integration step, the independent variable (\(V\)) and the dependent variables (\(\dot{n}_A\), \(\dot{n}_D\), \(\dot{n}_U\), and \(T\)) will be known, as will the given and known constants listed in the assignment summary. I will need to calculate any other quantities that appear in the IVODE design equations. Here that means I’ll need to calculate the rates, and I can do so the same way as for the CSTR design equations.
For case (b), where the PFR is first, the initial and final values in Table 15.1 will again be known. I’ll again need to evaluate the derivatives at the start of each integration step, and doing so will be the same as it was in case (a).
Then, having solved the PFR design equations, I will know the molar flow rates and temperature for stream 1, so the only unknowns in the CSTR residuals expressions will again be the variables labeled “out” and the two rates. Consequently, I can solve the CSTR design equations just as I did in case (a), except that the rate must be evaluated at the conditions of stream 2.
As noted when the reactor design equations were generated, this is a liquid phase system, so the volumetric flow rate is constant and equal to \(\dot{V}_0\).
Ancillary Equations for Evaluating the Residuals for Case (a)
\[ \dot{n}_{A,in} = \dot{n}_{A,0} = \dot{V}_0 C_{A,0} \tag{13} \]
\[ \dot{n}_{D,in} = \dot{n}_{D,0} = 0 \tag{14} \]
\[ \dot{n}_{U,in} = \dot{n}_{U,0} = 0 \tag{15} \]
\[ T_{in} = T_0 \tag{16} \]
\[ r_1 = k_{0,1} \exp{\left( \frac{-E_1}{RT_1} \right)} \frac{\dot{n}_{A,1}}{\dot{V}_0} \tag{17} \]
\[ r_2 = k_{0,2} \exp{\left( \frac{-E_2}{RT_1} \right)} \left(\frac{\dot{n}_{A,1}}{\dot{V}_0}\right)^2 \tag{18} \]
Ancillary Equations for Evaluating the Residuals for Case (b)
At the point where equations (5) through (8) need to be solved in case (b), the PFR design equations will have been solved to find values of \(V\), \(\dot{n}_A\), \(\dot{n}_D\), \(\dot{n}_U\), and \(T\) spanning the range from their values at the PFR inlet to the PFR outlet. The ancillary equations for evaluating the CSTR residuals are then given in equations (19) through (24).
\[ \dot{n}_{A,in} = \dot{n}_{A,1} = \dot{n}_A \big\vert_{V=V_{PFR}} \tag{19} \]
\[ \dot{n}_{D,in} = \dot{n}_{D,1} = \dot{n}_D \big\vert_{V=V_{PFR}} \tag{20} \]
\[ \dot{n}_{U,in} = \dot{n}_{U,1} = \dot{n}_U \big\vert_{V=V_{PFR}} \tag{21} \]
\[ T_{in} = T_1 = T \big\vert_{V=V_{PFR}} \tag{22} \]
\[ r_1 = k_{0,1} \exp{\left( \frac{-E_1}{RT_2} \right)} \frac{\dot{n}_{A,2}}{\dot{V}_0} \tag{23} \]
\[ r_2 = k_{0,2} \exp{\left( \frac{-E_2}{RT_2} \right)} \left(\frac{\dot{n}_{A,2}}{\dot{V}_0}\right)^2 \tag{24} \]
Ancillary Equations for Evaluating the Derivatives for Both Cases
\[ r_1 = k_{0,1} \exp{\left( \frac{-E_1}{RT} \right)} \frac{\dot{n}_A}{\dot{V}_0} \tag{25} \]
\[ r_2 = k_{0,2} \exp{\left( \frac{-E_2}{RT} \right)} \left(\frac{\dot{n}_A}{\dot{V}_0}\right)^2 \tag{26} \]
When the CSTR is first, case (a), the molar flows and temperature for stream 2 are found from the solution to the PFR design equations. When the PFR is first, the molar flows and temperature for stream 2 will be calculated when the CSTR design equations are solved. In both cases, the conversion and selectivity can then be calculated using their defining equations.
Ancillary Equations for Calculating the Quantities of Interest
In case (a) the molar flows and temperature for stream 2 can be found from the solution of the PFR design equations as shown in equations (27) - (30). In case (b), the molar flows and temperature for stream 2 will have been found when the CSTR design equations were solved. In both cases the conversion and selectivity then can be calculated using equations (31) and (32).
\[ \dot{n}_{A,2} = \dot{n}_A \big\vert_{V=V_{PFR}} \tag{27} \]
\[ \dot{n}_{ D,2} = \dot{n}_D \big\vert_{V=V_{PFR}} \tag{28} \]
\[ \dot{n}_{U,2} = \dot{n}_U \big\vert_{V=V_{PFR}} \tag{29} \]
\[ T_2 = T \big\vert_{V=V_{PFR}} \tag{30} \]
\[ f_A = \frac{\dot{n}_{A,0} - \dot{n}_{A,2}}{\dot{n}_{A,0}} \tag{31} \]
\[ S_{D/U} = \frac{\dot{n}_{D,2}}{\dot{n}_{U,2}} \tag{32} \]
Calculations Summary
- Substitute given and known constants into all equations.
- When it is necessary to evaluate the derivatives
- \(V\), \(\dot{n}_A\), \(\dot{n}_D\), \(\dot{n}_U\), and \(T\) will be available.
- Calculate \(r_1\) and \(r_2\) using equations (25) and (26).
- Evaluate and return the derivatives using equations (9) through (12).
- When it is necessary to evaluate the residuals
- Set \(\dot{n}_{A,in}\), \(\dot{n}_{D,in}\), \(\dot{n}_{U,in}\), and \(T_{in}\) using equations (13) through (16) for case (a) or (19) through (22) for case (b).
- Guesses for \(\dot{n}_{A,out}\), \(\dot{n}_{D,out}\), \(\dot{n}_{U,out}\), and \(T_{out}\) will be available.
- Calculate \(r_1\) and \(r_2\) using equations (17) and (18) for case (a) or equations (23) and (24) for case (b).
- Evaluate the residuals, \(\epsilon_1\), \(\epsilon_2\), \(\epsilon_3\), and \(\epsilon_4\) using equations (5) through (8).
- When it is necessary to calculate the quantities of interest, [list]
- for case (a),
- corresponding sets of values of \(V\), \(\dot{n}_A\), \(\dot{n}_D\), \(\dot{n}_U\), and \(T\), spanning the range from their initial values to their final values will be available.
- calculate \(\dot{n}_{A,2}\), \(\dot{n}_{D,2}\), \(\dot{n}_{U,2}\), and \(T_2\) using equations (27) through (30).
- calculate the conversion and selectivity using equations (31) and (32).
- for case (a),
15.4.1.3 Numerical implementation of the Solution
- Make the given and known constants available for use in all functions.
- Define variables to hold \(\dot{n}_{A,in}\), \(\dot{n}_{D,in}\), \(\dot{n}_{U,in}\), and \(T_{in}\) and make them available to all functions.
- Write a derivatives function that
- receives the independent and dependent variables, \(V\), \(\dot{n}_A\), \(\dot{n}_D\), \(\dot{n}_U\), and \(T\), as arguments,
- evaluates the derivatives as described in step 2 of the calculations summary, and returns them.
- Write a residuals function that
- receives a guess for \(\dot{n}_{A,out}\), \(\dot{n}_{D,out}\), \(\dot{n}_{U,out}\), and \(T_{out}\),
- evaluates the residual as described in step 3 of the calculations summary, and returns their values
- Write a cstr model function that
- receives the initial guess for \(\dot{n}_{A,out}\), \(\dot{n}_{D,out}\), \(\dot{n}_{U,out}\), and \(T_{out}\),
- calls an ATE solver passing the initial guess and the name of the residuals function from step 4 as arguments
- receives a solution of the CSTR design equations
- checks that the ATE solver converged, and
- returns the solution returned by the ATE solver.
- Write a pfr model function that
- receives the initial values in Table 15.1 as an argument,
- gets corresponding sets of values of \(V\), \(\dot{n}_A\), \(\dot{n}_D\), \(\dot{n}_U\), and \(T\), spanning the range from their initial values to their final values by calling an IVODE solver and passing the following information to it
- the appropriate initial values and stopping criterion in Table 15.1 and
- the name of the derivatives function from step 3 above, d, checks that the solver successfully solved the IVODEs, and
- returns the values returned by the IVODE solver.
- Perform the analysis by
- setting \(\dot{n}_{A,in}\), \(\dot{n}_{D,in}\), \(\dot{n}_{U,in}\), and \(T_{in}\) for case (a), equations (13) through (16),
- solving the CSTR design equations by calling the cstr model function from step 5,
- solving the PFR design equations by calling the pfr model function from step 6, passing the appropriate initial values from Table 15.1 as an argument,
- calculating the quantities of interest for case (a) as described in step 5 of the calculations summary,
- solving the PFR design equations by calling the pfr model function from step 6, passing the appropriate initial values from Table 15.1 as an argument,
- setting \(\dot{n}_{A,in}\), \(\dot{n}_{D,in}\), \(\dot{n}_{U,in}\), and \(T_{in}\) for case (b,) equations (19) through (22),
- solving the CSTR design equations by calling the cstr model function from step 5,
- calculating the quantities of interest for case (b) as described in step 5 of the calculations summary, and
- displaying the results.
15.4.1.4 Results and Discussion
The calculations were performed as described above. When the CSTR is the first reactor, the conversion is 75% and the selectivity is 2.63 mol D per mol U. If the PFR is first, the conversion is 65.7% and the selectivity is 2.76 mol D per mol U. This trade-off might have been expected on the basis of some qualitative reasoning.
The reactions are exothermic with typical kinetics, so a large rate, and correspondingly high conversion, is favored by high temperature and high reactant concentration. The reactions occur in parallel, and the instantaneous selectivity, \(S_{D/U}\), is the ratio of the desired to undesired reaction rates, as given in equation (33). Examination of that equation shows that high selectivity also is favored by high temperature (because \(E_2 - E_1\) is a positive number), but by low reactant concentration (due to the \(\frac{1}{C_A}\) term).
\[ S_{D/U} = \frac{r_D}{r_U} = \frac{k_{0,1} \exp{\left( \frac{-E_1}{RT_1} \right)}C_A}{k_{0,2} \exp{\left( \frac{-E_2}{RT_1} \right)} C_A^2} = \frac{k_{0,1}}{k_{0,2}} \exp{ \left( \frac{E_2 - E_1}{RT} \right)}\frac{1}{C_A} \tag{33} \]
The temperature and the composition within the reactors are coupled through the reactor design equations. It isn’t possible to change one without affecting the other. When the type of the first reactor is changed, that affects the temperature and composition in both reactors. As such, it isn’t surprising that there is a trade-off between conversion and selectivity.
15.4.2 Water-Gas Shift in Series PFRs with Cooling Between the Reactors
The water-gas shift, equation (1), is exothermic, \(\Delta H\) = –9120 cal mol-1, and reversible. The equilibrium constant can be approximated using equation (2) with \(K_{0,1}\) = 0.132. The heat capacities of CO, H2O, CO2, H2, and inert, I, can be take to be constant and equal to 29.3, 34.3, 41.3, 29.2, and 40.5 J mol-1 K-1, respectively. Two packed bed reactors in series are used to process a feed consisting of 1 mol CO h-1, 0.359 mol CO2 h-1, 4.44 mol H2 h-1, 0.180 mol I h-1, and 9.32 mol H2O h-1 at 26 atm and 445 °C. The volume of the first packed bed is 685 cm3, and it is packed with a high-temperature catalyst for which the rate is given by equation (3) with \(k_{0,1}\) = 0.0354 mol cm-3 min-1 atm-2 and \(E_1\) = 9740 cal mol-1. The product stream leaving the first packed bed passes through a heat exchanger. Chilled water at 20 °C flowing at a rate of 1100 g/h enters the other side of the heat exchanger and exits the heat exchanger at 50 °C The volume of the second packed bed is 3950 cm3, and is packed with a low-temperature catalyst for which the rate also is given by equation (3), but with \(k_{0,1}\) = 1.77 x 10-3 mol cm-3 min-1 atm-2 and \(E_1\) = 3690 cal mol-1. Pressure drop in the reactors is negligible. What are the overall conversion of CO and the temperature of the product gas leaving the second packed bed reactor?
\[ CO + H_2O \rightleftarrows CO_2 + H_2 \tag{1} \]
\[ K_1 = K_{0,1} \exp{ \left( \frac{-\Delta H}{RT} \right)} \tag{2} \]
\[ r_1 = k_1 \left( P_{CO} P_{H_2O} - \frac{P_{CO_2}P_{H_2}}{K_1} \right) \tag{3} \]
The thermodynamic and kinetic parameters presented in this example are approximations. They should only be used in this assignment and not for any other purpose.
This assignment describes two packed bed reactors in series with a heat exchanger between them. I’ll sketch the system, labeling the reactors, heat exchanger, and flow streams. I’ll use “R” with a number to denote the reactors, “HE” to denote the heat exchanger, and I’ll simply number the streams. Then I can use the labels as I summarize the assignment.
15.4.2.1 Assignment Summary
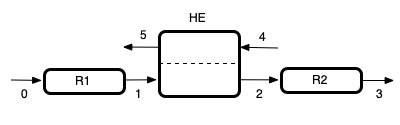
Given and Known Constants: \(\Delta H\) = –9120 cal mol-1, \(K_{0,1}\) = 0.132, \(C_{p,CO}\) = 29.3 J mol-1 K-1, \(C_{p,H_2O}\) = 34.3 J mol-1 K-1, \(C_{p,CO_2}\) = 41.3 J mol-1 K-1, \(C_{p,H_2}\) = 29.2 J mol-1 K-1, \(C_{p,I}\) = 40.5 J mol-1 K-1, \(\dot{n}_{CO,0}\) = 1 mol h-1, \(\dot{n}_{CO_2,0}\) = 0.359 mol h-1, \(\dot{n}_{H_2,0}\) = 4.44 mol h-1, \(\dot{n}_{I,0}\) = 0.180 mol h-1, \(\dot{n}_{H_2O,0}\) = 9.32 mol h-1, \(P\) = 26 atm, \(T_0\) = 445 °C, \(V_{R1}\) = 685 cm3, \(k_{0,R1}\) = 0.0354 mol cm-3 min-1 atm-2, \(E_{R1}\) = 9740 cal mol-1, \(T_4\) = 20 °C, \(\dot{m}_4\) = 1100 g min-1, \(T_5\) = 50 °C, \(V_{R2}\) = 3950 cm3, \(k_{0,R2}\) = 1.77 x 10-3 mol cm-3 min-1 atm-2, and \(E_{R2}\) = 3690 cal mol-1.
Reactor System: Adiabatic, steady-state PFRs configured as shown in Figure 15.3.
Quantities of Interest: \(f_{CO}\) and \(T_3\).
15.4.2.2 Mathematical Formulation of the Solution
This assignment involves two reactors and a heat exchanger. I need to generate reactor design equations for the reactors and mole and energy balances for the heat exchanger. The reactors are both adiabatic PFRs, so I can use the same reactor design equations for both of them. There is neglibible pressure drop, so the mole balances and an energy balance on the reacting gas comprise the reactor design equations. The reactor diameters and lengths are not provided, but by noting that \(dV = \frac{\pi D^2}{4}dz\), I can write the design equations using the reaactor volume as the independent variable. The general form of the steady-state PFR mole balance is given in Equation 6.39. In this system there is only one reaction taking place, so the sum becomes a single term.
\[ \frac{d \dot{n}_i}{d z} =\frac{\pi D^2}{4}\sum_j \nu_{i,j}r_j \qquad \Rightarrow \qquad \frac{d \dot{n}_i}{dV} = \nu_{i,1}r_1 \]
The general form of the steady-state PFR energy balance is given in Equation 6.40. The reactors are adiabatic, so the heat transfer term goes to zero. The summations can be expanded, and the IVODE can be rearranged in the form of a derivative expression.
\[ \left(\sum_i \dot{n}_i \hat{C}_{p,i} \right) \frac{d T}{d z} = \pi D U\left( T_{ex} - T \right) - \frac{\pi D^2}{4}\sum_j r_j \Delta H_j \]
\[ \frac{d T}{dV} = \frac{-r_1 \Delta H_1}{\dot{n}_{CO} \hat{C}_{p,CO} + \dot{n}_{H_2O} \hat{C}_{p,H_2O} + \dot{n}_{CO_2} \hat{C}_{p,CO_2} + \dot{n}_{H_2} \hat{C}_{p,H_2} + \dot{n}_{I} \hat{C}_{p,I}} \]
Reactor Design Equations
Mole balance design equations for CO, H2O, CO2, H2, and I in either of the reactors are presented in equations (4) through (8). The energy balance on the reacting fluid is given in equation (9).
\[ \frac{d \dot{n}_{CO}}{dV} = - r_1 \tag{4} \]
\[ \frac{d \dot{n}_{H_2O}}{dV} = - r_1 \tag{5} \]
\[ \frac{d \dot{n}_{CO_2}}{dV} = r_1 \tag{6} \]
\[ \frac{d \dot{n}_{H_2}}{dV} = r_1 \tag{7} \]
\[ \frac{d \dot{n}_{I}}{dV} = 0 \tag{8} \]
\[ \frac{d T}{dV} = \frac{-r_1 \Delta H_1}{\dot{n}_{CO} \hat{C}_{p,CO} + \dot{n}_{H_2O} \hat{C}_{p,H_2O} + \dot{n}_{CO_2} \hat{C}_{p,CO_2} + \dot{n}_{H_2} \hat{C}_{p,H_2} + \dot{n}_{I} \hat{C}_{p,I}} \tag{9} \]
The number of dependent variables in the IVODEs (4) - (9) is equal to the number of equations, so the IVODEs can be solved. To do so, initial values and a stopping criterion are needed. For each reactor, I can define \(V=0\) to be the reactor inlet. In that case the initial values are simply the values of the dependent variables at the reactor inlet. For the first reactor, those are the feed values given for stream 0. For the second reactor, those are the values for stream 2. In each case the reactor volume is known and can be used as the stopping criterion.
Initial Values and Stopping Criterion for Reactor R1
| Variable | Initial Value | Stopping Criterion |
|---|---|---|
| \(V\) | \(0\) | \(V_1\) |
| \(\dot{n}_{CO}\) | \(\dot{n}_{CO,0}\) | |
| \(\dot{n}_{H_2O}\) | \(\dot{n}_{H_2O,0}\) | |
| \(\dot{n}_{CO_2}\) | \(\dot{n}_{CO_2,0}\) | |
| \(\dot{n}_{H_2}\) | \(\dot{n}_{H_2,0}\) | |
| \(\dot{n}_{I}\) | \(\dot{n}_{I,0}\) | |
| \(T\) | \(T_0\) |
Initial Values and Stopping Criterion for Reactor R2
| Variable | Initial Value | Stopping Criterion |
|---|---|---|
| \(V\) | \(0\) | \(V_2\) |
| \(\dot{n}_{CO}\) | \(\dot{n}_{CO,2}\) | |
| \(\dot{n}_{H_2O}\) | \(\dot{n}_{H_2O,2}\) | |
| \(\dot{n}_{CO_2}\) | \(\dot{n}_{CO_2,2}\) | |
| \(\dot{n}_{H_2}\) | \(\dot{n}_{H_2,2}\) | |
| \(\dot{n}_{I}\) | \(\dot{n}_{I,2}\) | |
| \(T\) | \(T_2\) |
I also need mole and energy balances on the heat exchanger. Quite simply, streams 1 and 2 are equal in composition, Equation 15.7. The same is true of streams 4 and 5, but since I’m given the mass flow and the fluid is pure water, I’ll use a mass balance. The energy balance is given by Equation 15.9. The rate at which heat is added to stream 4 is given by Equation 15.12, and the rate it is added to stream 1 is given by Equation 15.10. Combining yields the energy balance for the system. Since the heat capacities are constant, the integrals can be evaluated.
\[ \dot{n}_{i,1} = \dot{n}_{i,2} \]
\[ \dot{m}_4 = \dot{m}_5 \]
\[ \begin{align} 0 &= \sum_i \left( \dot{n}_{i,1} \int_{T_1}^{T_2}\hat{C}_{p,i} dT\right) - \dot{m}_4 \int_{T_4}^{T_5} \tilde{C}_{p,H_2O_{(l)}} dT \\ &= \left( \dot{n}_{CO,1}\hat{C}_{p,CO} + \dot{n}_{H_2O,1}\hat{C}_{p,H_2O} + \dot{n}_{CO_2,1}\hat{C}_{p,CO_2} + \dot{n}_{H_2,1}\hat{C}_{p,H_2} + \dot{n}_{I,1}\hat{C}_{p,I} \right)\left(T_2 - T_1\right)\\ &- \dot{m}_4\tilde{C}_{p,H_2O_{(l)}} \left( T_5 - T_4\right) \end{align} \]
Mole and Energy Balances on the Heat Exchanger
Mole and mass balances on the heat exchanger are shown in equations (10) through (15). An energy balance on the heat exchanger is given in equation (16).
\[ \dot{n}_{CO,1} = \dot{n}_{CO,2} \tag{10} \]
\[ \dot{n}_{H_2O,1} = \dot{n}_{H_2O,2} \tag{11} \]
\[ \dot{n}_{CO_2,1} = \dot{n}_{CO_2,2} \tag{12} \]
\[ \dot{n}_{H_2,1} = \dot{n}_{H_2,2} \tag{13} \]
\[ \dot{n}_{I,1} = \dot{n}_{I,2} \tag{14} \]
\[ \dot{m}_4 = \dot{m}_5 \tag{15} \]
\[ \begin{align} 0 &= \left( \dot{n}_{CO,1}\hat{C}_{p,CO} + \dot{n}_{H_2O,1}\hat{C}_{p,H_2O} + \dot{n}_{CO_2,1}\hat{C}_{p,CO_2} + \dot{n}_{H_2,1}\hat{C}_{p,H_2} + \dot{n}_{I,1}\hat{C}_{p,I} \right)\left(T_2 - T_1\right)\\ &- \dot{m}_4\tilde{C}_{p,H_2O_{(l)}} \left( T_5 - T_4\right) \end{align} \tag{16} \]
The reactor design equations are IVODEs. In order to solve them numerically I’ll need to do two things: calculate the values of the derivatives at the start of each integration step and calculate all of the initial and final values in Table 15.2 and Table 15.2. At the start of each integration step, the independent variable \(V\) and dependent variables, \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\), will be known, as will the given and known constants listed in the assignment summary. I will need to calculate any other quantities that appear in the IVODE design equations. In this case, the only other quantities appearing in the IVODEs is the rate, \(r_1\). It can be calculated using equation (3), but before that can be done, \(k_1\), \(K_1\), \(P_{CO}\), \(P_{H_2O}\), \(P_{CO_2}\), and \(P_{H_2}\) must be calculated. \(k_1\) can be calculated using the Arrhenius expression, Equation 4.8, and \(K_1\) can be calculated using equation (2). The partial pressures can be calculated using the definition of a partial pressure.
\[ P_i = y_iP = \frac{\dot{n}_i}{\dot{n}_{CO} + \dot{n}_{H_2O} + \dot{n}_{CO_2} + \dot{n}_{H_2} + \dot{n}_{I}}P \]
Ancillary Equations for Evaluating the Derivatives
The rate, \(r_1\) can be calculated using equation (3). The rate coefficient can be calculated using equation (17), the partial pressures of the reactants and products using equations (18) - (21), and \(K_1\) using equation (2). In equation (17) the pre-exponential factor and activation energy for the appropirate reactor must be used.
\[ k_1 = k_{0,Rx} \exp{\left( \frac{-E_{Rx}}{RT} \right)} \tag{17} \]
\[ P_{CO} =\frac{\dot{n}_{CO}}{\dot{n}_{CO} + \dot{n}_{H_2O} + \dot{n}_{CO_2} + \dot{n}_{H_2} + \dot{n}_{I}}P \tag{18} \]
\[ P_{H_2O} =\frac{\dot{n}_{H_2O}}{\dot{n}_{CO} + \dot{n}_{H_2O} + \dot{n}_{CO_2} + \dot{n}_{H_2} + \dot{n}_{I}}P \tag{19} \]
\[ P_{CO_2} =\frac{\dot{n}_{CO_2}}{\dot{n}_{CO} + \dot{n}_{H_2O} + \dot{n}_{CO_2} + \dot{n}_{H_2} + \dot{n}_{I}}P \tag{20} \]
\[ P_{H_2} =\frac{\dot{n}_{H_2}}{\dot{n}_{CO} + \dot{n}_{H_2O} + \dot{n}_{CO_2} + \dot{n}_{H_2} + \dot{n}_{I}}P \tag{21} \]
All of the initial and final values in Table 15.2 are known, so the reactor design equations for R1 can be solved to obtain corresponding sets of values of \(V\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\) spanning the range from the reactor inlet to the reactor outlet. The values at the reactor outlet are the molar flow rates and temperature for stream 1.
The molar flow rates for stream 2 can then be calculated using equations (10) through (14). The mass flow rate of stream 5 can be calculated using equation (15). The temperature of stream 2 can then be calculated using equation (16). Upon doing so, all of the initial and final values in Table 15.3 will be known.
The reactor design equations for reactor R2 then can be solved to obtain corresponding sets of values of \(V\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\) spanning the range from the reactor inlet to the reactor outlet. The values at the reactor outlet are the molar flow rates and temperature for stream 3.
Ancillary Equations for Calculating the Quantities of Interest
The outlet temperature will be found upon solving the reactor design equations for reactor R2. The overall conversion can be calculated using equation (22).
\[ f_{CO} = \frac{\dot{n}_{CO,0} - \dot{n}_{CO,3}}{\dot{n}_{CO,0}} \tag{22} \]
Calculations Summary
- Substitute given and known constants into all equations.
- When it is necessary to evaluate the derivatives
- \(V\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\) will be available.
- use \(k_{0,Rx}\) and \(E_{Rx}\) for the reactor being modeled to calculate \(k_1\) using equation (17).
- calculate \(K_1\), \(P_{CO}\), \(P_{H_2O}\), \(P_{CO_2}\), and \(P_{H_2}\) using equations (2) and (18) - (21).
- calculate \(r_1\) using equation (2).
- evaluate the derivatives using equations (4) - (9).
- When it is necessary to solve the heat exchanger mole and energy balances,
- calculate the molar flow rates for stream 2 using equations (10) - (14).
- calculate \(\dot{m}_5\) using equation (15).
- calculate \(T_2\) using equation (16).
- When it is necessary to calculate the overall conversion, \(f_{CO}\)
- corresponding sets of values of \(V\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\), spanning the range from the reactor inlet to the reactor outlet.
- use the value of \(\dot{n}_{CO}\) at the reactor outlet as \(\dot{n}_{CO,3}\) and calculate \(f_{CO}\) using equation (22).
15.4.2.3 Numerical implementation of the Solution
- Make the given and known constants available for use in all functions.
- Define a variable to hold a flag representing the reactor currently being modeled and make it available to all functions.
- Write a derivatives function that
- receives the independent and dependent variables, \(V\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\), as arguments,
- evaluates the derivatives as described in step 2 of the calculations summary, and returns them.
- Write a reactor model function that
- receives the initial values in Table 15.2 or Table 15.3, and the reactor volume (final value) as arguments,
- gets corresponding sets of values of \(V\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\),, spanning the range from their initial values to their final values by calling an IVODE solver and passing the following information to it
- the initial values and stopping criterion in Table 15.2 or Table 15.3 and
- the name of the derivatives function from step 3 above, d, checks that the solver successfully solved the IVODEs, and
- returns the values returned by the IVODE solver.
- Perform the analysis by
- setting the flag to indicate reactor R1 is being analyzed.
- calling the reactor model function from step 4 above to get corresponding sets of values of \(V\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\), spanning the range from the reactor inlet to the reactor outlet,
- setting the molar flow rates and temperature of stream 1 equal to the reactor R1 outlet values,
- solving the heat exchanger mole and energy balances as described in step 3 of the calculations summary to get the molar flow rates and temperature of stream 2
- setting the flag to indicate reactor R2 is being analyzed.
- calling the reactor model function from step 4 above to get corresponding sets of values of \(V\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\), spanning the range from the reactor inlet to the reactor outlet,
- calculating the conversion using equation (22).
15.4.2.4 Results and Discussion
The calculations were performed as described above. The outlet temperature, in stream 3, is 246 °C, and the conversion is 99.4 %. A configuration like that shown in Figure 15.3 is used in commercial water-gas shift systems. There are several catalysts available for the reaction. Some are active and stable at higher temperatures (325 to 500 °C), some at lower temperatures (180 to 250 °C), and some at lower steam to CO ratios. However, none of the catalysts alone are capable of practically reaching high CO conversion in a single reactor.
The high temperature catalysts offer a greater reaction rate, which reduces the reactor volume. However, the equilibrium constant decreases with increasing temperature. As a consequence, equilibrium prevents the system from reaching high CO conversion in a single reactor. The low temperature catalysts operate at temperatures where equilibrium does not prevent high CO conversion. However, the adiabatic temperature rise that accompanies the reaction limits the conversion. At high conversion in a single reactor, the temperature increases to the maximum that the catalyst can withstand and prevents proceeding to high conversion. In addition, the rates at the lower temperatures are smaller resulting in larger reactor volumes. Catalysts that con operate a lower steam to CO ratios also become limited by the adiabatic temperature rise. Operating at lower steam to CO decreases the equilibrium conversion and it causes the reactor temperature to rise faster.
A system like that depicted in Figure 15.3 circumvents the problems associated with a single reactor system. Reactor R1 uses a high-temperature catalyst and converts the majority of the CO. Because the temperature is high, the rate is large and that keeps the volume of reactor R1 smaller. The product from reactor R1 is cooled and fed to reactor R2 which uses a low-temperature catalyst. While the rate is smaller in reactor R2, equilibrium does not limit the conversion, and because much of the conversion is accomplished in reactor R1, the temperature rise in reactor R2 does not exceed the maximum temperature the catalyst can withstand.
The system examined in this assignment is not optimized. Typically dry feed composition and the final conversion of CO are fixed based upon the intended use of the hydrogen. A multi-dimensional optimization can be performed to find the process parameters that minimize the total volume of the reactors. The optimization variables include the steam to CO ratio in stream 0, the temperature of stream 0, the conversion in reactor R1, and the temperature of stream 2.
15.4.3 Minimizing the Total Volume of Two CSTRs in Series
An aqueous solution at 30 °C containing A and B at concentrations of 1.0 and 1.2 M, respectively, is to be fed to two CSTRs in series at a flow rate of 75 L min-1. Reaction (1) will occur in the adiabatic reactors with a rate of reaction that is accurately described by equation (2). The rate coefficient exhibits Arrhenius temperature dependence with a pre-exponential factor of 8.72 x 105 L mol-1 min-1 and an activation energy of 7200 cal mol-1. The heat of reaction (1) is -10,700 cal mol-1 and may be assumed to be constant. The heat capacity of the solution and the density of the solution may be taken to be constant and equal to those of water (1.0 cal g-1 K-1 and 1.0 g cm-3). If 90% of the A needs to be converted, what is the minimum total volume required, and how is it divided between the two reactors?
\[ A + B \rightarrow Y + Z \tag{1} \]
\[ r_1 = k_1 C_A C_B \tag{2} \]
This assignment involves two CSTRs operating in series. To begin, I’ll sketch the system and label the reactors and flow streams. Then, as I summarize the assignment, I can use the stream number and reactor labels as subscripts on variables to indicate the stream or reactor to which they correspond.
15.4.3.1 Assignment Summary
Network Schematic

Given and Known Constants: \(T_0\) = 30 °C, \(C_{A,0}\) = 1.0 mol l-1, \(C_{B,0}\) = 1.2 mol l-1, \(\dot{V}_0\) = 75 L min-1, \(k_{0,1}\) = 8.72 x 105 L mol-1 min-1, \(E_1\) = 7200 cal mol-1, \(\Delta H_1\) = -10,700 cal mol-1, \(\tilde{C}_p\) = 1.0 cal g-1 K-1, \(\rho\) = 1.0 g cm-3, \(f_A\) = 0.9, \(R\) = 1.987 cal mol-1 K-1.
Reactor System: Two adiabatic, steady-state CSTRs in series
Quantities of Interest: \(V_{min}\), \(V_{R1,opt}\), and \(V_{R2,opt}\).
15.4.3.2 Mathematical Formulation of the Solution
The only equipment in this system is the two reactors. I’ll need to generate the reactor design equations needed to model them. Since they are both steady-state adiabatic CSTRs and are processing the same set of reagents, the design equations needed to model them will be the same and will consist of mole balances on each of the reagents and an energy balance on the reacting fluid. Here I’ll use “in” and “out” to label the flow streams entering and leaving the reactor.
The general form of the steady-state CSTR mole balance is given in Equation 6.31, and in this system there is only one reaction occurring. I’ll use \(V_{Rx}\) to represent the volume of the reactor where \(x\) can be either 1 or 2.
\[ 0 = \dot{n}_{i,in} - \dot{n}_{i,out} + V_{Rx} \sum_j \nu_{i,j}r_j = \dot{n}_{i,in} - \dot{n}_{i,out} + V_{Rx} \nu_{i,1}r_1 \]
The general form of the steady-state CSTR energy balance is given in Equation 6.32. The reactors in this system are adiabatic (\(\dot{Q} = 0\)) and do no work (\(\dot{W} = 0\)). The assignment provides the gravimetric heat capacity of the reacting fluid as a whole, so the term for the sensible heat can be written using that heat capacity. It is constant so it can be taken outside of the integral and the integral can be evaluated. As for the mole balances, there is only one reaction taking place. Both non-zero terms are preceded by minus signs, so I’ll multiply both sides of the equation by -1. Finally, the reacting fluid is a liquid and may be assumed to be incompressible, so I’ll use \(\dot{V}_0\) as the volumetric flow rate since it is the same in all three streams.
\[ 0 = \cancelto{0}{\dot{Q}} - \cancelto{0}{\dot{W}} - \cancelto{\rho \dot{V}_0 \tilde{C}_p \left(T_{out} - T_{in} \right)}{\sum_i\dot{n}_{i,in} \int_{T_{in}}^T \hat{C}_{p,i}dT} - V_{Rx} \sum_j r_j \Delta H_j \]
\[ 0 = \rho \dot{V}_0 \tilde{C}_p \left(T_{out} - T_{in} \right) + V_{Rx} r_1 \Delta H_1 \]
All of the reactor design equation above are written in the form of residual expressions in anticipation of solving them numerically. All together there are 10 reactor design equations (five for each reactor), so I can solve them to find the values of 10 unknown quantities. Very often the design equations are solved to find the outlet flow rates and temperature, but here the conversion of A, and hence \(\dot{n}_{A,2}\) is known, so instead I’ll use the volume of reactor R1 as an unknown.
Reactor Design Equations
Mole balance design equations for A, B, Y, and Z in reactor R1 are presented in equations (3) through (6). The energy balance on the reacting fluid in reactor R1 is given in equation (7). The corresponding reactor design equations for reactor R2 are presented in equations (8) - (12). These ten equations can be solved to find the ten unknowns: \(\dot{n}_{A,1}\), \(\dot{n}_{B,1}\), \(\dot{n}_{Y,1}\), \(\dot{n}_{Z,1}\), \(T_1\) \(V_{R1}\), \(\dot{n}_{B,2}\), \(\dot{n}_{Y,2}\), \(\dot{n}_{Z,2}\), \(T_2\)
\[ 0 = \dot{n}_{A,0} - \dot{n}_{A,1} - V_{R1} r_{1,R1} = \epsilon_1 \tag{3} \]
\[ 0 = \dot{n}_{B,0} - \dot{n}_{B,1} - V_{R1} r_{1,R1} = \epsilon_2 \tag{4} \]
\[ 0 = \dot{n}_{Y,0} - \dot{n}_{Y,1} + V_{R1} r_{1,R1} = \epsilon_3 \tag{5} \]
\[ 0 = \dot{n}_{Z,0} - \dot{n}_{Z,1} + V_{R1} r_{1,R1} = \epsilon_4 \tag{6} \]
\[ 0 = \rho \dot{V}_0 \tilde{C}_p \left(T_1 - T_0 \right) + V_{R1} r_{1,R1} \Delta H_1 = \epsilon_5 \tag{7} \]
\[ 0 = \dot{n}_{A,1} - \dot{n}_{A,2} - V_{R2} r_{1,R2} = \epsilon_6 \tag{8} \]
\[ 0 = \dot{n}_{B,1} - \dot{n}_{B,2} - V_{R2} r_{1,R2} = \epsilon_7 \tag{9} \]
\[ 0 = \dot{n}_{Y,1} - \dot{n}_{Y,2} + V_{R2} r_{1,R2} = \epsilon_8 \tag{10} \]
\[ 0 = \dot{n}_{Z,1} - \dot{n}_{Z,2} + V_{R2} r_{1,R2} = \epsilon_9 \tag{11} \]
\[ 0 = \rho \dot{V}_0 \tilde{C}_p \left(T_2 - T_1 \right) + V_{R2} r_{1,R2} \Delta H_1 = \epsilon_{10} \tag{12} \]
In this assignment, the reactor design equations will be solved for \(\dot{n}_{A,1}\), \(\dot{n}_{B,1}\), \(\dot{n}_{Y,1}\), \(\dot{n}_{Z,1}\), \(T_1\) \(V_{R1}\), \(\dot{n}_{B,2}\), \(\dot{n}_{Y,2}\), \(\dot{n}_{Z,2}\), \(T_2\). In order to solve the ATEs numerically I’ll need to do two things: provide an initial guess for the solution and evaluate the residuals them each time an improved guess is generated.
At that point, guesses for each of the unknowns will be available along with the given and known constants listed in the assighment summary. I will need to calculate any other quantities that appear in the residuals expressions. Examining equations (3) through (12) shows that I’ll need to calculate \(\dot{n}_{A,2}\), the rate of reaction (1) in each of the two reactors (\(r_{1,R1}\) and \(r_{1,R2}\)) and the volume of reactor R2, \(V_{R2}\).
I know the inlet molar flow rate of A and the conversion, so calculating \(\dot{n}_{A,2}\) is trivial.
The rate in each reactor can be calculated using equation (2), noting that the rate coefficient and the concentrations are those of the outlet stream from that reactor. The rate coefficient can be calculated using the Arrhenius expression, Equation 4.8, and the concentrations using the defining equation for concentration in a flow system, Equation 2.15. When calculating the concentrations the volumetric flow rate can be set equal to \(\dot{V}_0\) since it is the same in all three flow streams.
I can’t write an explicit expression for the volume of reactor R2, but I do know that the total reactor volume must be minimized. So, I can choose a range of values for \(V_{R2}\), solve the reactor design equations for each value and choose the value that corresponds to the minimum total reactor volume.
Ancillary Equations for Evaluating the Residuals
\[ \dot{n}_{A,2} = \dot{n}_{A,0} \left( 1 - f_A \right) \tag{13} \]
\[ r_{1,R1} = k_{0,1} \exp{ \left( \frac{-E_1}{RT_1} \right) } \left( \frac{\dot{n}_{A,1}}{\dot{V}_0} \right) \left( \frac{\dot{n}_{B,1}}{\dot{V}_0} \right) \tag{14} \]
\[ r_{1,R2} = k_{0,1} \exp{ \left( \frac{-E_1}{RT_2} \right) } \left( \frac{\dot{n}_{A,2}}{\dot{V}_0} \right) \left( \frac{\dot{n}_{B,2}}{\dot{V}_0} \right) \tag{15} \]
\[ V_{R2,opt} = \underset{V_{R2}}{\arg\min}\left( V_{R1} +V_{R2} \right) \tag{16} \]
When I solve the ATEs numerically, I’ll also need to provide an initial guess for the solution. To complete this assignment, I’m going to choose a range of values for \(V_{R2}\), solve the reactor design equations for each value, and then find the value where the total volume is smallest. Since I’ll start with the smallest value of \(V_{R2}\) in the range, I expect that most of the conversion will take place in the first reactor. Since I know the overall conversion of A is 90%, I can make good guesses for the outlet molar flow rates from the second reactor. For the temperatures I’ll just guess there is a small increase, and for the volume, I’ll guess a volume for reactor R1 that’s in the middle of the range of values for \(V_{R2}\). If I have difficulty converging the calculations, I may need to alter these guesses. Once I solve the reactor design equations for the first value of \(V_{R2}\) in the range, I can use the result as the guess for the next value in the range.
Ancillary Equations for Calculating the Quantities of Interest
The reactor design equations will be solved using a range of values of \(V_{R2}\). This will yield a corresponding value of \(V_{R1}\) for each value in the range. The optimum value of \(V_{R2}\) will be the one where the total volume is minimized, equation (16). The optimum value of \(V_{R1}\) can then be calculated using equation (17).
\[ V_{R1,opt} = V_{min} - V_{R2,opt} \tag{17} \]
Calculations Summary
- Substitute given and known constants into all equations.
- When it is necessary to evaluate the residuals
- \(\dot{n}_{A,1}\), \(\dot{n}_{B,1}\), \(\dot{n}_{Y,1}\), \(\dot{n}_{Z,1}\), \(T_1\) \(V_{R1}\), \(\dot{n}_{B,2}\), \(\dot{n}_{Y,2}\), \(\dot{n}_{Z,2}\), \(T_2\) will be available together with the constants listed in the assignment summary and a value of \(V_{R2}\).
- calculate \(\dot{n}_{A,2}\), \(r_{1,R1}\), and \(r_{1,R2}\) using equations (13) - (15).
- evaluate the residuals, \(\epsilon_1\) through \(\epsilon_{10}\) using equations (3) through (12)
- When it is necessary to calculate the quantities of interest
- a range of values of \(V_{R2}\) and the corresponding values of \(V_{R1}\) will be available.
- identify the optimum reactor R2 volume, \(V_{R2,opt}\), for which the total volume, \(V_{R1}\) + \(V_{R2}\), is minimized (equation (16)),
- calculate \(V_min\) (the sum of the optimum reactor R2 volume and the corresponding reactor R1 volume),
- calculate \(V_{R1,opt}\) using equation (17).
15.4.3.3 Numerical implementation of the Solution
- Make the given and known constants available for use in all functions.
- Make \(V_{R2}\) available to all functions
- Write a residuals function that
- receives guess values for \(\dot{n}_{A,1}\), \(\dot{n}_{B,1}\), \(\dot{n}_{Y,1}\), \(\dot{n}_{Z,1}\), \(T_1\) \(V_{R1}\), \(\dot{n}_{B,2}\), \(\dot{n}_{Y,2}\), \(\dot{n}_{Z,2}\), \(T_2\),
- evaluates and returns the residuals as described in step 2 of the calculations summary.
- Write a reactor model function that
- receives an initial guess for the unknowns, \(\dot{n}_{A,1}\), \(\dot{n}_{B,1}\), \(\dot{n}_{Y,1}\), \(\dot{n}_{Z,1}\), \(T_1\) \(V_{R1}\), \(\dot{n}_{B,2}\), \(\dot{n}_{Y,2}\), \(\dot{n}_{Z,2}\), and \(T_2\) as an argument,
- gets a set of values of the unknowns that solve the ATEs by calling an ATE solver and passing the following information to it
- the initial guess and
- the name of the residuals function from step 2 above, d, checks that the solver converged, and
- returns the values returned by the ATE solver.
- Perform the analysis by
- defining a range of values of \(V_{R2}\)
- defining an initial guess for the unknowns, \(\dot{n}_{A,1}\), \(\dot{n}_{B,1}\), \(\dot{n}_{Y,1}\), \(\dot{n}_{Z,1}\), \(T_1\) \(V_{R1}\), \(\dot{n}_{B,2}\), \(\dot{n}_{Y,2}\), \(\dot{n}_{Z,2}\), and \(T_2\) for the first value of \(V_{R2}\) in the range,
- for each value of \(V_{R2}\) in the range
- making that value available to all functions,
- calculating the corresponding value of \(V_{R1}\) by calling the reactor model function in step 4 above,
- setting the initial guess equal to the results from step ii.
- calculating the optimum volumes of reactors R1 and R2 and the minimum total volume as described in step 3 of the calculations summary.
15.4.3.4 Results and Discussion
The calculations were performed as described above. The optimum volumes of reactors R1 and R2 are 48 L and 60.3 L, respectively. The minimum total reactor volume then is 108 L. fig-example_15_4_3_volume_plot shows the variation in the total reactor volume as the volume of reactor R2 changes.
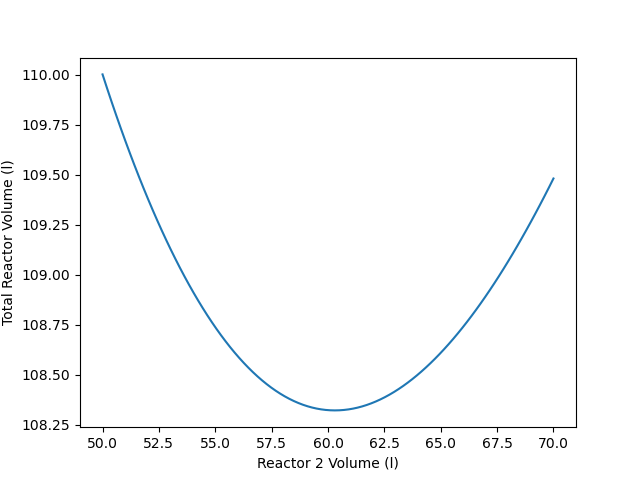
It is easy to understand why there is a minimum total volume when two adiabatic CSTRs operate in series with a fixed overall conversion and a fixed feed rate. When an exothermic reaction takes place adiabatically, thermal effects and composition effects oppose each other as the reaction time, or equivalently, the conversion, increases. As a consequence, as the reaction time or the conversion increases, the reaction rate may increase, reach a maximum, and then decrease. (See Example 9.6.1.)
As long as the final conversion from the two steady-state, adiabatic CSTRs in series is greater than the conversion where the rate is at its maximum, the rate will decrease as the conversion increases. In the present assignment, that means that the rate at 90% overall conversion, \(r_{90\%}\), is smaler than the rate at, say, 85% conversion, \(r_{85\%}\).
\[ r_{90\%} < r_{85\%} \]
Now consider the two CSTRs in Figure 15.4, and suppose that reactor R1 is vanishingly small. When that is true, the reacting fluid will spend very, very little time in reactor R1. (The time spent in the reactor is the volume divided by the fixed volumetric flow rate, \(\dot{V}_0\), and here the volume is nearly zero.) In this situation all of the A must be converted in reactor R2, and it operates at the lowest rate. The reaction time, \(\tau_{R2}\) will equal the amount converted in reactor R2, \(0.9 \dot{n}_{A,0}\) divided by the rate in reactor R2, and the volume of reactor R2 will equal the product of the reaction time and the fixed volumetric feed rate. Since the volume of reactor R1 is zero, the total volume in this first scenario, \(V_{\text{scenario }1}\), is just the volume of reactor R2.
\[ \tau_{R2} = \frac{0.9 \dot{n}_{A,0}}{r_{90\%}} \qquad \Rightarrow \qquad V_{R2} = \dot{V}_0 \frac{0.9 \dot{n}_{A,0}}{r_{90\%}} \]
\[ V_{\text{scenario }1} = \dot{V}_0 \frac{0.9 \dot{n}_{A,0}}{r_{90\%}} \]
Next reconsider the two CSTRs in Figure 15.4, but suppose that reactor R2 is vanishingly small. By the same reasoning, in this case all of the reaction must take place in reactor R1, and it will operate at the lowest rate. In other words, the reaction time and volume of reactor R1 in this scenario will equal those of reactor R2 in the preceeding scenario.
\[ \tau_{R1} = \frac{0.9 \dot{n}_{A,0}}{r_{90\%}} \qquad \Rightarrow \qquad V_{R1} = \dot{V}_0 \frac{0.9 \dot{n}_{A,0}}{r_{90\%}} \]
\[ V_{\text{scenario }2} = \dot{V}_0 \frac{0.9 \dot{n}_{A,0}}{r_{90\%}} \]
Those two scenarios represent the extremes on the spectrum of reactor sizes. In the first scenario reactor R1 accounted for 0% of the total reactor volume, and in the second scenario reactor R1 accounted for 100% of the total reactor volume. Additionally, the total reactor volume is the same for both scenarios.
Finally, consider the situation where reactor R1 operates at 85% overall conversion and reactor R2 operates at 90% overall conversion. Clearly, this scenario is intermediate between secenarions 1 and 2 because reactor R1 accounts for more than 0%, but less than 100%, of the total reactor volume. In this scenario the amount of A converted in reactor R1 is \(0.85 \dot{n}_{A,0}\) and the amount converted in reactor R2 is \(0.05 \dot{n}_{A,0}\). The volumes of the two reactors can then be added to find the total volume for this scenario.
\[ V_{\text{scenario }3} = V_{R1} + V_{R2} = \dot{V}_0 \frac{0.85 \dot{n}_{A,0}}{r_{85\%}} + \dot{V}_0 \frac{0.05 \dot{n}_{A,0}}{r_{90\%}} \]
The expression for the total reactor volume for secenario 1 or secenario 2 can be split into two terms.
\[ V_{\text{scenario }1} = \dot{V}_0 \frac{0.85 \dot{n}_{A,0}}{r_{90\%}} + \dot{V}_0 \frac{0.05 \dot{n}_{A,0}}{r_{90\%}} \]
Comparing the total volume for scenario 1 to the total volume for secnario 3, the second terms in the expressions are equal. However, the first term in the expression for scenario 3 is smaller than that for scenario 1 because \(r_{85\%}\) is larger than \(r_{90\%}\).
These three scenarios show that there must be a minimum total reactor volume. That is, starting from the extreme where reactor R1 represents 0% of the total reactor volume and moving to the intermediate scenario results in a decrease in the total volume. Then, upon moving to the other extreme, the total reactor volume increases. Thus, while the intermediate point may not be the minimum total reactor volume, the fact that it is smaller than either of the extremes shows that there must be a minimum total volume somewhere between the extremes.
It is important to note that the preceding qualitative analysis assumed that the final overall conversion was greater than the conversion where the rate reaches its maximum value. If, instead, the final overall conversion was less than or equal to the conversion where the rate is at its maximum, then the rate at all other overall conversions would be smaller than the rate at the final overall conversion. By the same reasoning as used above, in this case the smallest total reactor volume would correspond to a single CSTR operating at the final overall conversion.
As formulated here, the completion of the assignment required the reactor design equations for the two reactors to be solved simultaneously. An alternative approach would be to choose a range of values of \(V_{R1}\), calculate the corresponding values of \(V_{R1}\) by solving the design equations, and finding the optimum volumes as was done above. With that approach, for each value of \(V_{R1}\), the design equations for reactor R1 could have been solved independently and then, using the results, the design equations for reactor R2 could have been solved.
15.4.4 Comparing Two Unequally Sized PFRs in Parallel with Equal Flows and Equal Space Times
A liquid phase process that uses a 60 dm3 PFR is going to be shut down so that a second 40 dm3 PFR can be added to increase throughput. Space constraints dictate that the second reactor will be added in parallel with the first. The design calls for processing a feed solution containing 1 mol L-1 of A at 60 °C and flowing at a rate of 0.55 dm3 min-1. The solution density may be assumed to be constant. The reactors will operate adiabatically, at steady state, and with negligible pressure drop. The reaction is irreversible, and the reaction rate is given in equation (2) where k0 = 2.63 x 107 L mol-1 min-1 and E = 62 kJ mol-1. The heat of reaction and the heat capacity of the solution may be assumed to be constant and equal to -35 kJ mol-1 and 800 J L-1 K-1, respectively. Compare the conversion when the feed is split equally between the two reactors to the conversion when the feed is split so that the space times are equal in the two reactors.
\[ 2 A \rightarrow Y + Z \tag{1} \]
\[ r_1 = k_1 C_A^2 \tag{2} \]
This assignment features two PFRs in parallel. I’ll begin by making a schematic diagram and labeling the equipment. I’ll use R1 and R2 to represent the reactors, S to represent the stream splitter, and M to represent the stream mixer. I’ll simply number the flow streams. I can then use the labels as subscripts on variables to indicate the equipment or flow stream to which they correspond.
15.4.4.1 Assignment Summary
Network Schematic
Given and Known Constants: \(V_{PFR,1}\) = 60 dm3, \(V_{PFR,1}\) = 40 dm3, \(C_{A,0}\) = 1 mol L-1, \(T_0\) = 60 °C, \(\dot{V}_0\) = 0.55 dm3 min-1, \(k_{0}\) = 2.63 x 107 L mol-1 min-1, \(E\) = 62 kJ mol-1, \(\Delta H_1\) = -35 kJ mol-1, \(\breve{C}_p\) = 800 J L-1 K-1, and \(R\) = 8.314 J mol-1 K-1.
Reactor System: Two adiabatic, steady-state PFRs in parallel.
Quantities of Interest: \(f_A\) for \(\dot{V}_1 = \dot{V}_1\) and for \(\tau_{R1} = \tau_{R2}\).
15.4.4.2 Mathematical Formulation of the Solution
This assignment involves a reactor network with two PFRs a stream splitter and a stream mixer. The PFRs are both adiabatic and operate at steady-state with negligible pressure drop. They are processing the same feed, differing only in the volumetric flow rate entering the PFR and the PFR volume. I can generate one set of reactor design equations to model both PFRs. I’ll just need to set the inlet volumetric flow rate and the reactor volume to the appropriate values.
The general form of the steady-state PFR mole balance is given in Equation 6.39. For this assignment I don’t know the reactor lengths or diameters, only their volumes. However, since they are adiabatic, I can re-write the equations using the reactor volume as the dependent variable. After doing that by noting that \(dV = \frac{\pi D^2}{4}dz\), I won’t need to know the diameters or lengths. At the same time, I can expand the summation over the reactions. Here it will expand to a single term.
\[ \frac{d \dot{n}_i}{d z} =\frac{\pi D^2}{4}\sum_j \nu_{i,j}r_j \]
\[ \frac{d \dot{n}_i}{dV} = \nu_{i,1}r_1 \]
The general form of the steady-state PFR reacting fluid energy balance is given in equation Equation 6.40. Since the reactors are adiabatic, the heat transfer term goes to zero. After eliminating it, I can again re-write the equation using the reactor volume as the dependent variable. At the same time, I can expand the sum over the reactions, and I can re-write the sensible heat term using the volumetric heat capacity provided in the problem statement. Finally, I can rearrange the equation into the form of a derivative expression.
\[ \cancelto{\dot{V}\breve{C}_p}{\left(\sum_i \dot{n}_i \hat{C}_{p,i} \right)} \frac{d T}{d z} = \cancelto{0}{\pi D U\left( T_{ex} - T \right)} - \frac{\pi D^2}{4}\cancelto{r_1 \Delta H_1}{\sum_j r_j \Delta H_j} \]
\[ \frac{dT}{dV} = \frac{- r_1 \Delta H_1}{\dot{V} \breve{C}_p} \]
The reacting fluid in this system is a liquid. It can be assumed to be incompressible in which case the volumetric flow rate appearing in the enerby balance will equal the inlet volumetric flow rate. That is, when modeling reactor R1, it will equal \(\dot{V}_1\), and when modeling reactor R2, it will equal \(\dot{V}_2\)
Since there is negligible pressure drop, I don’t need to write a momentum balance on the PFR. I’ll likely also need mole and energy balances on the stream splitter and the stream mixer. I’m not going to write them at this point, but instead will wait until I need them.
Reactor Design Equations
Mole balance design equations on A, Y, and Z for either PFR are presented in equations (3), (4), and (5), and an energy balance on the reacting fluid is given in equation (6).
\[ \frac{d \dot{n}_A}{dV} = -2r_1 \tag{3} \]
\[ \frac{d \dot{n}_Y}{dV} = r_1 \tag{4} \]
\[ \frac{d \dot{n}_Z}{dV} = r_1 \tag{5} \]
\[ \frac{dT}{dV} = \frac{- r_1 \Delta H_1}{\dot{V} \breve{C}_p} \tag{6} \]
The reactor design equations for each PFR are IVODEs. There are four of them and they contain four dependent variables, so I don’t need to add an IVODE or eliminate a dependent variable. Since they are IVODEs, I do need initial values and a stopping criterion, though.
For either reactor, I can define \(V=0\) to be the inlet to the reactor, and then I can use the volume of the reactor as the stopping criterion. With this definition, the initial values are simple the values of the dependent variables at the reactor inlet. The feed to the process, stream 0, does not contain Y or Z, and neither will the two streams, 1 and 2, formed by splitting it. Thus for each of the reactor the initial values of the molar flow rates of Y and Z are equal to zero.
Initial Values and Stopping Criterion
| Variable | Initial Value | Stopping Criterion |
|---|---|---|
| \(V\) | \(0\) | \(V_{PFR,1}\) |
| \(\dot{n}_A\) | \(\dot{n}_{A,1}\) | |
| \(\dot{n}_Y\) | \(0\) | |
| \(\dot{n}_Z\) | \(0\) | |
| \(T\) | \(T_1\) |
| Variable | Initial Value | Stopping Criterion |
|---|---|---|
| \(V\) | \(0\) | \(V_{PFR,2}\) |
| \(\dot{n}_A\) | \(\dot{n}_{A,2}\) | |
| \(\dot{n}_Y\) | \(0\) | |
| \(\dot{n}_Z\) | \(0\) | |
| \(T\) | \(T_2\) |
In order to solve the IVODEs numerically I’ll need to do two things: calculate the values of the derivatives at the start of each integration step and calculate all of the initial and final values in Table 15.4 and Table 15.5.
At the start of each integration step, the independent variable, \(V\), and dependent variables, \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\) will be known, as will the given and known constants listed in the assighment summary. I will need to calculate any other quantities that appear in the IVODE design equations (3) through (6).
Examining those equations I see that I will need to calculate \(r_1\) and \(\dot{V}\). This is a liquid phase system, so assuming the liquid to be incompressible, the liquid flow rate will be constant. The value of \(\dot{V}\) will depend upon which of the two reactors I’m modeling and which of the two cases I’m analyzing. Here I’ll just consider the two reactors. If I’m modeling reactor R1, then \(\dot{V} = \dot{V}_1\), and if I’m modeling reactor R2, \(\dot{V} = \dot{V}_2\).
The rate can be calculated using equation (2), but to do so I first need to calculate the rate coefficient using the Arrhenius expression, Equation 4.8, and the concentration of A. The concentration of A is equal to the molar flow rate of A divided by the volumetric flow rate in the reactor being modeled.
\[ k_1 = k_0 \exp{ \left( \frac{-E}{RT} \right)} \]
\[ C_A = \frac{\dot{n}_A}{\dot{V}} \]
Ancillary Equations for Evaluating the Derivatives for Reactor R1
\[ \dot{V} = \dot{V}_1 \tag{7} \]
\[ r_1 = k_0 \exp{ \left( \frac{-E}{RT} \right)} \frac{\dot{n}_A^2}{\dot{V}_1} \tag{8} \]
Ancillary Equations for Evaluating the Derivatives for Reactor R2
\[ \dot{V} = \dot{V}_2 \tag{9} \]
\[ r_1 = k_0 \exp{ \left( \frac{-E}{RT} \right)} \frac{\dot{n}_A^2}{\dot{V}_2} \tag{10} \]
When I solve the IVODEs numerically, I’ll also need to calculate the initial and final values in Table 15.4 and Table 15.5. The volumes of the two reactors are known. The splitter does not change the temperature, so the temperatures of streams 1 and 2 are equal to the temperature of stream 0.
The splitter also does not change the concentration, so the concentration of A in streams 1 and 2 are equal to the concentration of A in stream 0. The molar flow rate in those streams is that concentration times the volumetric flow rate.
For the first case, the volumetric flow rates of streams 1 and 2 are equal. Based on a mass balance on the splitter, the flow rates of streams 1 and 2 must sum to equal the flow rate of stream 0. So, the flow rates of streams 1 and 2 are each equal to one half the flow rate of stream 0. Multiplying by the concentration of A gives the molar flow rates of A for the first case.
\[ \dot{n}_{A,1} = \dot{n}_{A,2} = 0.5 \dot{V}_0 C_{A,0} \]
For the second case, the space times are equal.
\[ \tau_{R1} = \tau_{R2} \]
I can substitute the definition of a space time and again make use of the splitter mass balance requirement that the volumetric flow rate of stream 0 must equal the combined flow rates of streams 1 and 2. Rearranging then gives me expressions for the volumetric flow rates.
\[ \frac{V_{PFR,1}}{\dot{V}_1} = \frac{V_{PFR,2}}{\dot{V}_2} = \frac{V_{PFR,2}}{\dot{V}_0 - \dot{V}_1} \]
\[ \frac{V_{PFR,1}}{V_{PFR,2}}\left( \dot{V}_0 - \dot{V}_1 \right) = \dot{V}_1 \]
\[ \dot{V}_1 = \frac{V_{PFR,1}}{V_{PFR,2}}\frac{\dot{V}_0}{1 + \frac{V_{PFR,1}}{V_{PFR,2}}} = \dot{V}_0 \frac{V_{PFR,1} }{V_{PFR,1} + V_{PFR,2}} \]
\[ \dot{V}_2 = \dot{V}_0 - \dot{V}_1 = \dot{V}_0 \left( 1 - \frac{V_{PFR,1} }{V_{PFR,1} + V_{PFR,2}} \right) \]
As before, the molar flow rates of A are simply the concentration of A multiplied by the volumetric flow rate.
\[ \dot{n}_{A,1} = \dot{V}_0 \frac{V_{PFR,1} }{V_{PFR,1} + V_{PFR,2}} C_{A,0} \]
\[ \dot{n}_{A,2} = \dot{V}_0 \left( 1 - \frac{V_{PFR,1} }{V_{PFR,1} + V_{PFR,2}} \right) C_{A,0} \]
Ancillary Equations for Calculating the Initial and Final Values for the Equal Flow Case
\[ T_1 = T_0 \tag{11} \]
\[ T_2 = T_0 \tag{12} \]
\[ \dot{V}_1 = 0.5\dot{V}_0 \tag{13} \]
\[ \dot{V}_2 = 0.5\dot{V}_0 \tag{14} \]
\[ \dot{n}_{A,1} = 0.5 \dot{V}_0 C_{A,0} \tag{15} \]
\[ \dot{n}_{A,2} = 0.5 \dot{V}_0 C_{A,0} \tag{16} \]
Ancillary Equations for Calculating the Initial and Final Values for the Equal Space Time Case
\[ T_1 = T_0 \tag{17} \]
\[ T_2 = T_0 \tag{18} \]
\[ \dot{V}_1 = \dot{V}_0 \frac{V_{PFR,1} }{V_{PFR,1} + V_{PFR,2}} \tag{19} \]
\[ \dot{V}_2 = \dot{V}_0 \left( 1 - \frac{V_{PFR,1} }{V_{PFR,1} + V_{PFR,2}} \right) \tag{20} \]
\[ \dot{n}_{A,1} = \dot{V}_0 \frac{V_{PFR,1} }{V_{PFR,1} + V_{PFR,2}} C_{A,0} \tag{21} \]
\[ \dot{n}_{A,2} = \dot{V}_0 \left( 1 - \frac{V_{PFR,1} }{V_{PFR,1} + V_{PFR,2}} \right) C_{A,0} \tag{22} \]
At this point the reactor design equations can be solved numerically for each reactor to get corresponding sets of values of \(V\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\) spanning the range from their initial (inlet) values to their final (outlet) values. Thus, solving the design equations yields the molar flow rate of A in stream 3 and in stream 4.
The conversion can be calculated using its definition, but to do so the molar flow rate of A in stream 5 must first be calculated. That can be done using a mole balance on the stream mixer for reagent A.
Ancillary Equations for Calculating the Quantities of Interest
Solving the reactor design equations for each reactor yields corresponding sets of values \(V\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\) spanning the range from the reactor inlet to the reactor outlet. The molar flow rate of reagent A at the outlet of reactor R1 is \(\dot{n}_{A,3}\), and that for reagent B is \(\dot{n}_{A,5}\). With those resu lts, the over all conversion can be calculated.
\[ \dot{n}_{A,5} = \dot{n}_{A,3} + \dot{n}_{A,4} \tag{23} \]
\[ f_A = \frac{\dot{n}_{A,0} - \dot{n}_{A,5}}{\dot{n}_{A,0}} \tag{24} \]
Calculations Summary
- Substitute given and known constants into all equations.
- if the equal flow case is being analyzed, calculate the temperatures, volumetric flow rates, and molar flow rates of reagent A for streams 1 and 2 using equations (11) - (16).
- if the equal space time case is being analyzed, calculate the temperatures, volumetric flow rates, and molar flow rates of reagent A for streams 1 and 2 using equations (17) - (22).
- When it is necessary to evaluate the derivatives
- \(V\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\) will be available.
- calculate \(\dot{V}\) and \(r_1\) using equations (7) and (8) for reactor R1 or equations (9) and (10) for reactor R2.
- calculate the derivatives using equations (3) through (6)
- When it is necessary to calculate the initial and final values in Table 15.4 and Table 15.5 all of the values will be known either because they were given or because they were calculated in step 1.
- When it is necessary to calculate the quantities of interest,
- \(V\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\) spanning the range from the reactor inlet to the reactor outlet.
- The molar flow rate of reagent A at the outlet of reactor R1 is \(\dot{n}_{A,3}\), and that for reagent B is \(\dot{n}_{A,5}\).
- calculate \(\dot{n}_{A,5}\) using equation (23), then calculate \(f_A\) using equation (24).
15.4.4.3 Numerical implementation of the Solution
- Make the given and known constants available for use in all functions.
- Define a variable to hold \(\dot{V}\) and make it available to all functions.
- Write a derivatives function that
- receives the independent and dependent variables, \(V\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\), as arguments,
- evaluates the derivatives as described in step 2 of the calculations summary, and returns them.
- Write a reactor model function that
- receives the volume of the reactor being modeled as an argument.
- calculates the initial and final values in Table 15.4 or Table 15.5 as described in step 3 of the calculations summary,
- gets corresponding sets of values of \(V\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\), spanning the range from their initial values to their final values by calling an IVODE solver and passing the following information to it
- the initial values and stopping criterion in Table 15.4 or Table 15.5 and
- the name of the derivatives function from step 3 above, d, checks that the solver successfully solved the IVODEs, and
- returns the values returned by the IVODE solver.
- Perform the analysis by
- setting \(\dot{V}\) for reactor R1 and the equal flow case
- calling the reactor model function from step 4 above to get corresponding sets of values of \(V\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\) for reactor R1,
- setting \(\dot{V}\) for reactor R2 and the equal flow case
- calling the reactor model function from step 4 above to get corresponding sets of values of \(V\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\) for reactor R2,
- calculating the quantities of interest as described in step 4 of the calculations summary,
- repeating steps 5a through 5e for the equal space time case.
15.4.4.4 Results and Discussion
The calculations were performed as described above. When the flow to the two PFRs is equal, the conversion is 79.4%. When the space times in the two PFRs are equal, the conversion is 80.3%. While the difference in conversions in this example is small, the results nonetheless are consistent with the caveat that mixing stream of unequal conversion should be avoided.
The reason is easy to understand from a qualitative perspective. For a typical reaction, the rate gets smaller as the conversion increases. As a consequence, each additional increment of conversion requires a larger volume than the increment before it. When two streams of unequal conversion are mixed, the resulting stream will have a conversion intermediate between the two. If the stream with the higher conversion had only been converted to the after-mixing conversion, the reduction in reactor volume would be more than that needed to convert the stream with the lower conversion to the after-mixing conversion. In other words, the after-mixing conversion could have been attained using less total reactor volume.
15.5 Symbols used in Chapter 15
| Symbol | Meaning |
|---|---|
| \(f_i\) | Fractional conversion of reactant \(i\). |
| \(in\) | Subscript denoting a flow stream entering a piece of equipment. |
| \(k_j\) | Rate coefficient for reaction \(j\). |
| \(k_{0,j}\) | Arrhenius pre-exponential factor for rate coefficient \(k_j\). |
| \(\dot{m}\) | Mass flow rate; an additional subscript denotes the flow stream. |
| \(\dot{n}_I\) | Molar flow rate of reagent \(i\); an additional subscript denotes the flow stream. |
| \(out\) | Subscript denoting a flow stream leaving a piece of equipment. |
| \(r_j\) | Rate of reaction \(j\). |
| \(A\) | Heat transfer area. |
| \(C_i\) | Concentration of reagent \(i\); an additional subscript denotes the flow stream. |
| \(\hat{C}_{p,i}\) | Molar heat capacity of reagent \(i\). |
| \(\tilde{C}_{p,}\) | Gravimetric heat capacity. |
| \(\breve{C}_{p,}\) | Volumetric heat capacity. |
| \(E_j\) | Arrhenius activation energy for rate coefficient \(k_j\). |
| \(K_j\) | Equilibrium constant for reaction \(j\). |
| \(K_{0,j}\) | Pre-exponential factor for equilibrium constant \(K_j\) when expressed in the form of the Arrhenius expression. |
| \(P\) | Pressure. |
| \(P_i\) | Parial pressure of reagent \(i\). |
| \(\dot{Q}\) | Heat transfer rate; an additional subscript denotes the flow stream. |
| \(R\) | Ideal gas constant. |
| \(S_{X/Y}\) | Selectivity for reagent X over reagent Y. |
| \(T\) | Temperature; an additional subscript denotes the flow stream. |
| \(U\) | Heat transfer coefficient; a subscripted “LM” denotes it is based on the log-mean temperature difference, while “AM” denotes arithemetic mean. |
| \(V\) | Volume; an additional subscript denotes the equipment. |
| \(\dot{V}\) | Volumetric flow rate; an additional subscript denotes the flow stream. |
| \(\epsilon\) | Residual; an additional subscript is used to differentiate between multiple residuals. |
| \(\rho\) | Density. |
| \(\tau\) | Space time; an additional subscript denotes the reactor. |
| \(\Delta H_j\) | Heat of reaction \(j\). |
| \(\Delta T\) | Temperature difference; a subscripted “LM” denotes the log-mean temperature difference, while “AM” denotes arithemetic mean. |