13  PFR Analysis

The reactors examined in preceding chapters were all variants of a stirred tank, that is, they were perfectly mixed. This chapter considers a very different kind of continuous reactor, namely the plug flow reactor (PFR). PFRs are basically tubes through which reacting fluid flows and within which chemical reactions take place.

Figure 13.1: Simple schematic representation of a PFR.

13.1 PFR Characteristics

The distincitve characteristics of PFRs were summarized in Chapter 6, and they are presented in more detail in Appendix H. The biggest difference between PFRs and stirred tanks lies in the mixing. Stirred tanks are perfectly mixed at all times, so there are never any spatial variations of composition or temperature within the reactor. In contrast, the composition and temperature vary continuously along the length of a PFR as the reacting fluid flows through it. More specifically, as illustrated in Figure H.1, it is assumed that the fluid velocity in the axial distance does not vary in the radial direction. As a consequence, the fluid can be thought of as differentially thick disks that move from the reactor inlet to the outlet. There is perfect mixing in the radial direction (i. e. within each differentially thick disk) an no mixing at all in the axial direction (i. e. between disks).

Another difference between PFRs and CSTRs is that the pressure of the reacting fluid in a PFR can decrease as the fluid flows from the inlet to the outlet. When analyzing CSTRs it is assumed that pressure changes are negligible both between inlet and outlet and between the top and bottom of the fluid within the reactor.

In PFRs, heat is exchanged through the reactor walls. Commonly there is a concentric tube surrounding the reactor tube with heat exchange fluid flowing through the annular space. Alternatively, there may be many reactor tubes that all pass through a larger shell while heat exchange fluid flows through the shell. In some applications PFR tubes pass though a firebox within which some fuel is burned. In this situation the flue gases are the heat exchange fluid, and any PFR tubes that are within line of sight of the combustion flame are additionally heated radiantly. Reaction Engineering Basics only considers heat exchange with a fliud in a shell surrounding the PFR tube (see Chapter 6).

Being continuous flow reactors, PFRs can operate at steady-state or in a transient mode. At the minimum, transient operation occurs when the PFR is started up and shut down. Transient behavior will occur whenever a reactor input changes. Those changes can involve the flow rate, the feed composition, the feed temperature, the feed pressure, the heat exchange fluid flow rate, and the heat exchange fluid inlet temperature. Due to the nature of plug flow, PFR transients typically only last as long as it takes the reacting fluid to flow from the reactor inlet to its outlet.

PFRs are well-suited to high throughput production. They can also be used for reactions that require solid catalyst particles. The absence of axial mixing can be an advantage because, unlike a CSTR, the reactants are not immediately diluted due to mixing with the fluid already present in the reactor. As a consequence, the concentration of reactant is high at the inlet. High reactant concentration typically results in a high reaction rate and a smaller reactor volume.

The absence of axial mixing can also be a disadvantage if the reaction is exothermic with limited or no heat removal. Unlike a CSTR, where the feed is instantly heated to the outlet temperature upon entering the reactor, fluid enters a PFR at the feed temperature, and its temperature rises continuously as it flows through the reactor. The lower temperatures near the inlet typically result in a lower rate, and therefore a larger reactor is needed to accomplish a given extent of conversion.

Another disadvangage of PFRs is the fixed heat transfer area. As noted, heat exchange with a PFR is typically limited to occur through the reactor wall. Unlike CSTRs, it isn’ feasible to add coiled tubes containing flowing heat exchange fluid within the PFR tube. Similarly, circulating the reacting fluid through an external heat exchanger is not practical. In some situations it is possible to break one long PFR into several shorter PFRs with additional cooling between the shorter lengths of reactor.

13.2 PFR Operation

Like CSTRs, PFRs are normally designed to operate at steady state. When a PFR operates at steady state, the composition, temperature and pressure are all constant over time at any one axial position in the reactor. The temperature pressure and composition will be different at a different location, but at that location they again will be constant over time. Put differently, the steady-state composition, pressure and temperature in a PFR will vary spatitially, but not temporally.

PFRs must operate in transient modes when they are started up and shut down, and they will also undergo transient operation if any reactor input changes. The absence of axial mixing can result in “odd” transients that intuitively seem to be incorrect. This aspect of transient PFR operation is discussed later in the chapter.

13.3 Qualitative Analysis of Steady-State Reaction in a PFR

Chapter 12 pointed out that in a continuous reactor, the amount of time during which reaction occurs is equal to the amount of time that the fluid spends in the reactor. As a consequence, when qualitatively analyzing the performance of a continuous reactor, the effects of small changes in space time are considered. When that is done, the qualitative analysis of a PFR is essentially the same as a BSTR except that the space time is used instead of elapsed clock time.

Indeed, there is a relationship between BSTR reaction time and PFR space time. As already noted, each differential, disk-shaped element of fluid that enters a PFR flows through the reactor without mixing with the fluid that entered before it or the fluid that enters after it. Furthermore, being differentially thin and with perfect radial mixing in a PFR, that thin disk is essentially a small batch reactor that moves from the reactor inlet to the reactor outlet, as illustrated in Figure 13.2. From the perspective of that thin disk, the reaction time is equal to the time it takes to flow from the reactor inlet to the reactor outlet.

Figure 13.2: Analogy between reaction time in a BSTR and space time in a PFR.

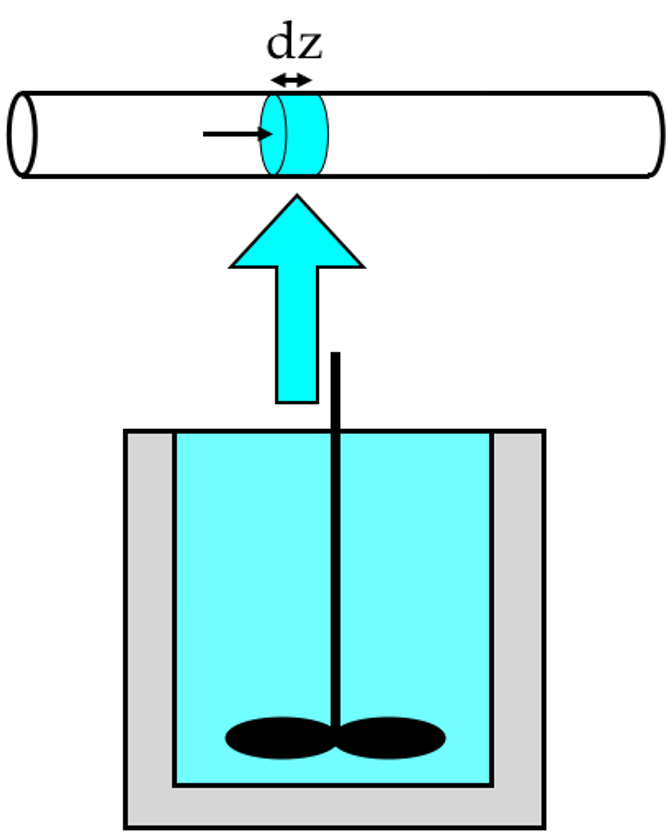
For incompressible liquid phase systems, the analogy of Figure 13.2 is exact. For gases, the volume of the thin disk may change as it moves through the reactor due to changes in temperature, pressure or total moles. The space time is defined in terms of the inlet volumetric flow rate, so it does not account for expansion or contraction of the thin disk. Nonetheless, for the purposes of a qualitative analysis the expansion effect is not important.

Section 9.3 presented an approach to qualitative analysis of a BSTR wherein the effects of small increments in reaction time were assessed. The same procedure can be used for PFR, substituting the space time for the reaction time. Basically the changes experienced as a function of reaction time in a BSTR are the same as the changes experienced upon progressing from a PFR’s inlet to its outlet.

13.4 PFR Design Equations

The reactor design equations for PFRs and their simplification were presented in Chapter 6. The PFR reactor design equations are derived in Appendix H. The general PFR mole balance, Equation 6.33, energy balance, Equation 6.34, and momentum balance, Equation 6.37, are reproduced below, along with energy balances on a perfectly mixed heat exchange fluid that exchanges sensible heat, Equation 6.2, or latent heat, Equation 6.6, with the reacting fluid.

\[ \frac{\partial \dot{n}_i}{\partial z} + \frac{\pi D^2}{4\dot{V}} \frac{\partial\dot{n}_i}{\partial t} - \frac{\pi D^2\dot{n}_i}{4\dot{V}^2} \frac{\partial \dot{V}}{\partial t} =\frac{\pi D^2}{4}\sum_j \nu_{i,j}r_j \]

\[ \begin{split} \left(\sum_i \dot{n}_i \hat{C}_{p,i} \right) \frac{\partial T}{\partial z} +& \frac{\pi D^2}{4\dot{V}} \sum_i \left(\dot{n}_i \hat{C}_{p,i} \right) \frac{\partial T}{\partial t} - \frac{\pi D^2}{4} \frac{\partial P}{\partial t} \\ &= \pi D U\left( T_{ex} - T \right) - \frac{\pi D^2}{4}\sum_j r_j \Delta H_j \end{split} \]

\[ \frac{\partial \dot{V}}{\partial t} + \frac{4 \dot{V}}{\pi D^2} \frac{\partial \dot{V}}{\partial z} + \frac{\pi D^2}{4 \rho} \frac{\partial P}{\partial z} = - \frac{2 f \dot{V}^2}{\pi D^3} \]

\[ \rho_{ex} V_{ex} \tilde{C}_{p,ex}\frac{dT_{ex}}{dt} = -\dot{Q} - \dot{m}_{ex} \int_{T_{ex,in}}^{T_{ex}} \tilde{C}_{p,ex}dT \]

\[ \frac{\rho_{ex} V_{ex} \Delta H_{\text{latent},ex}^0}{M_{ex}} \frac{d \gamma}{dt} = - \dot{Q} - \gamma \dot{m}_{ex} \frac{\Delta H_{\text{latent},ex}^0}{M_{ex}} \]

The transient PFR design equations above are parital differential equations. They are presented here for completeness. Transient analysis of PFRs is not presented in Reaction Engineering Basics except for the special case, discussed later in the chapter, where a front propagates through the reactor.

When a PRF is operating at steady state, the time derivatives are equal to zero and the partial derivatives become ordinary derivatives. The general form of the steady-state PFR mole balance, Equation 6.39, energy balance, Equation 6.40, momentum balance, Equation 6.41, and packed bed momentum balance, Equation 6.42, are reproduced here.

\[ \frac{d \dot{n}_i}{d z} =\frac{\pi D^2}{4}\sum_j \nu_{i,j}r_j \]

\[ \left(\sum_i \dot{n}_i \hat{C}_{p,i} \right) \frac{d T}{d z} = \pi D U\left( T_{ex} - T \right) - \frac{\pi D^2}{4}\sum_j r_j \Delta H_j \]

\[ \frac{dP}{dz} = - \frac{4G}{\pi D^2} \frac{d \dot{V}}{dz} - \frac{fG^2}{2D \rho} \]

\[ \frac{{dP}}{{dz}} = - \frac{{1 - \varepsilon }}{{{\varepsilon ^3}}}\frac{{{G^2}}}{{\rho {\Phi _s}{D_p}}}\left[ {\frac{{150\left( {1 - \varepsilon } \right)\mu }}{{{\Phi _s}{D_p}G}} + 1.75} \right] \]

Some of the PFR reactor design equations contain more than one dependent variable. As a consequence it is sometimes necessary to add a differential equation or eliminate a dependent variable in order to solve the design equations. Differential forms of the ideal gas law, Equation 13.1 and Equation 13.2, can be used to do this.

\[ P \frac{\partial \dot{V}}{\partial t} + \dot{V} \frac{\partial P}{\partial t} - R \left( T \sum_i \frac{\partial \dot{n}_i}{\partial t} + \left( \sum_i \dot{n}_i \right) \frac{\partial T}{ \partial t} \right) = 0 \tag{13.1}\]

\[ P \frac{d \dot{V}}{dz} + \dot{V} \frac{dP}{dz} - R \left( T \sum_i \frac{d\dot{n}_i}{dz} + \left( \sum_i \dot{n}_i \right) \frac{dT}{dz} \right) = 0 \tag{13.2}\]

The sensible heat terms in the PFR energy balances above are written in terms of the molar heat capacities of the reagents. Those terms can also be expressed in terms of the overall volumetric or gravimetric heat capacity of the reacting fluid.

\[ \left(\sum_i \dot{n}_i \hat{C}_{p,i} \right) \frac{\partial T}{\partial z} \Leftrightarrow \rho \dot{V} \tilde{C}_p \frac{\partial T}{\partial z} \Leftrightarrow \dot{V} \breve{C}_p \frac{\partial T}{\partial z} \tag{13.3}\]

\[ \frac{\pi D^2}{4\dot{V}} \sum_i \left(\dot{n}_i \hat{C}_{p,i} \right) \frac{\partial T}{\partial t} \Leftrightarrow \frac{\pi D^2}{4}\rho \tilde{C}_p \frac{\partial T}{\partial t} \Leftrightarrow \frac{\pi D^2}{4} \breve{C}_p \frac{\partial T}{\partial t} \tag{13.4}\]

If the reacting fluid is an incompressible, ideal liquid mixture, the volumetric flow rate will be constant. Consequently its derivative with respect to either time or axial position will equal zero. The total heat transferred from the exchange fluid to the reacting fluid is given by Equation 13.5.

\[ \dot{Q} = \int_0^L \pi D U \left(T_{ex} - T \right)dz \tag{13.5}\]

When rate expressions are substituted into the PFR design equations, they will introduce concentrations or, for gases, partial pressures. For liquid phase reactions, the concentration can be expressed in terms of the dependent variables in the design equations using its defining equation. For gases the concentration or partial pressure can be expressed in terms of the molar amounts using the ideal gas law.

\[ C_i = \frac{\dot{n}_i}{\dot{V}} \]

\[ C_i = \frac{\dot{n}_i}{\sum_i \left(\dot{n}_i\right)}\frac{P}{RT} \qquad i = \text{ ideal gas} \]

\[ P_i = \frac{\dot{n}_i}{\sum_i \left(\dot{n}_i\right)}P \qquad i = \text{ ideal gas} \]

13.5 PFR Reaction Fronts

According to the ideal PFR model fluid is perfectly mixed in the radial direction, but it does not mix at all in the axial direction. Furthermore, the velocity in the axial direction does not vary across the reactor tube. Figures H.1 and 13.2 show that with these assumptions the fluid flow through the reactor can be envisioned as differentially thick disks that move through the reactor one after the other. These disks never mix with the disk ahead of them or with the disk behind them.

Under certain conditions, these assumptions can result in transient behavior where a “front” moves through the reactor. Specifically if the feed temperature or the feed composition (but not the feed flow rate) changes abruptly, none of the fluid already in the reactor is affected. This is illustrated in Figure 13.3 for the situation where there isn’t any reaction taking place within the reactor.

Figure 13.3: Development of a front in a PFR following an abrupt change in the feed temperature or composition. Gray shading indicates fluid with the temperature and composition prior to the feed change and turquoise indicates fluid with the temperature and composition after the feed change.

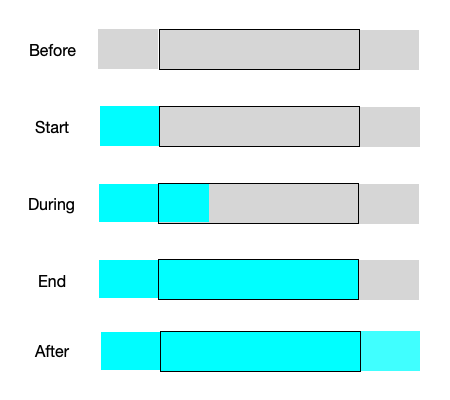
The figure indicates that there is an abrupt change, i. e. a step-change, in the feed temperature and/or composition that starts the transient response. Notice the sharp interface between the fluid that entered just before the change and the fluid entering to start the transient. That interface is called a “front”. As a result of the plug flow within the reactor, a short while later that front has moved part way through the reactor. It remains as sharp as it was at the instant the change occurred because the fluid just ahead of the front never mixes with the fluid at the beginning of the front.

The transient response of the reactor only lasts as long as it takes for the fluid to flow from the reactor inlet to the reactor outlet. If the fluid is incompressible, the linear velocity of the front is equal to the volumetric flow rate divided by the cross-sectional area of the tube, Equation 13.6. The position of the front is then equal to the elapsed time since the front began times the velocity, Equation 13.7. The duration of the front is then equal to the time at which the front reaches the reactor outlet at \(z=L\), which is equal to the PFR space time, Equation 13.8. Equations 13.6, 13.7, and 13.8 only apply for an incompressible fluid.

\[ v_{front} = \frac{\dot{V}}{\frac{\pi D^2}{4}} = \frac{4\dot{V}}{\pi D^2} \tag{13.6}\]

\[ z_{front} = v_{front} t = \frac{4\dot{V}t}{\pi D^2} \tag{13.7}\]

\[ L = \frac{4\dot{V}t_{transient}}{\pi D^2} \quad \Rightarrow \quad t_{transient} = \frac{\pi D^2}{4}\frac{L}{\dot{V}} = \frac{V_{PFR}}{\dot{V}} = \tau_{PFR} \tag{13.8}\]

The preceding discussion and Figure 13.3 assumed that no reaction was taking place when the step-change was applied to the feed composition and/or temperature. However, the same reasoning applies if reaction is taking place. The fluid ahead of the front is unaffected by the change in the feed, and similarly, the fluid behind the front is unaffected by the downstream presence of the front. In other words, the composition profile during this type of transient can be calculated using the steady-state PFR design equations.

When a step change in the composition and/or temperature occurs at the inlet to a steady-state PFR, a front will propagate along the length of the reactor. The concentration and temperature profile between the reactor inlet and the front is the steady-state profile for the new feed. The concentration and temperature profile between the front and the reactor outlet is the steady-state profile that existed before the feed change. Example 13.7.5 illustrates the propagation of this type of front.

It is important to understand that this approach only applies when the step change in the feed does not affect the fluid already in the reactor. If the feed flow rate changed, or if the exchange fluid flow rate or inlet temperature changed, a front like that described above would not result, and this type of analysis would not be valid.

13.6 Packed Bed PFRs

One of the advantages of PFRs is their suitability for heterogeneous catalystic reactions with solid catalysts. The catalyst takes the form of small particles, often cylindrical or spherical in shape with dimensions of the order of 0.25 in. The catalyst particles are highly porous. When they are examined using a microscope, they look similar to a common sponge, with interconnected void spaces throughout their volume.

13.6.1 The Pseudo-Homogeneous PFR Model

Stirred tank reactors are not will suited to reactions that require such catalysts due to the necessity of agitating the fluid to keep it perfectly mixed. Stirring a tank full of solid pellets is not practical. PFRs do not require agitation, so the interior of the reactor can be filled with the catalyst pellets. Screens or other similar means are used to keep the pellets in place, and the reacting fluid flows in the space between the pellets. That space is called the void space. Reactors packed with catalyst pellets as described here are known as packed bed PFRs (assuming they still obey the assumptions of the PFR model).

The presence of the packed bed does introduce a few complications. One is that the fluid no longer flows in the axial direction only. Its path must twist and turn so it can flow around the catalyst particles. In many cases, he relatively small amount of non-axial flow does not significantly affect the assumption of a constant velocity in the axial direction in any reactor cross-section, and it does not introduce significant radial mixing. This allows the reactor to be treated as a pseudo-homogeneous PFR, Figure 13.4.

Figure 13.4: In the pseudo-homogeneous PFR model (left), the entire reactor cross section is treated as if it is available for fluid flow (red), while in reality only the space between the (gray) catalyst particles is available.

13.6.2 Normalization of Heterogeneous Catalytic Reaction Rates

A second complication that arises due to the presence of a packed bed is related to the way the reaction rate is normalized. With homogeneous single-phase reactions, reaction rates are almost always normalized per unit volume of reacting fluid. Indeed, the reactor design equations used throughout Reaction Engineering Basics assume that the rate is normalized per reacting fluid volume, and the reacting fluid volume is essentially equal to the reactor volume.

Rate expressions for heterogeneous catalytic reactions are measured under conditions where concentration gradients (see below) are not significant. The reaction actually occurs on the surface of the catalyst particles. As such, the best way to normalize the rate is per unit catalyst surface area. Nonetheless, the catalyst surface area is not often used to normalize heterogeneous catalytic reaction rates. Most commonly the rates are normalized per unit mass of catalyst.

A few other normalization factors are sometimes used instead of the catalyst mass or surface area. Sometimes the rate is normalized per unit catalyst bed volume. When the pseudo-homogeneous PFR model is used, the catalyst bed volume is equal to the reactor volume. In other words, a rate normalized per unit catalyst bed volume can be used directly in the reactor design equations. However, the catalyst bed volume is not a very good normalization factor. It depends how tightly the catalyst particles are packed into the bed. That is, one could load the same mass of catalyst pellets into a tubular reactor three times and find three different bed volumes depending on how well the particles had settled into the tube.

Another potential normalization factor for heterogeneous catalytic reactions is the volume of pellets only. The pellet volume includes the pores within the individual particles, but not the space between particles. Assuming that the catalyst particles are manufactured with a consistent pore volume, this is an acceptable heterogeneous catalytic reaction rate normalziation factor.

The rate expression used to calculate the rate that is substituted into the reactor design equations must be normalized per bed volume. As just noted, this is not a common rate normalization factor due to variations in packing the bed. As such, it is more likely that the rate expression will be normalized per catalyst surface area, per catalyst mass, or per catalyst particle volume, in which case it must be renormalized for use in the design equations.

When the rate is normalized per unit catalyst mass, then the bed density must be measured when the catalyst is loaded into the reactor. Doing so is relatively straightforward. Before the catalyst is loaded into the reactor, the volume into which the catalyst will be loaded can be measured. The total mass of catalyst particles loaded into the reactor can then be measured. The bed density is simply the total mass of catalyst loaded divided by the volume into which it was loaded, Equation 13.9. The rate per catalyst mass can then be renormalized by multiplying it by the bed density, Equation 13.10.

\[ \rho_{bed} = \frac{m_{cat}}{V_{bed}} \tag{13.9}\]

\[ r_{\text{(per reactor volume)}} = \rho_{bed} r_{\text{(per catalyst mass)}} \tag{13.10}\]

There are experimental techniques and instruments for measuring the catalyst’s specific surface area, \(S_{cat}\), that is, the surface area per mass of catalyst. When the rate is normalized per catalyst surface area, it can be renormalized simply by multiplying it by the specific surface area to get the rate per catalyst mass, and then applying Equation 13.10, as shown in Equation 13.11.

\[ r_{\text{(per reactor volume)}} = \rho_{bed} S_{cat} r_{\text{(per catalyst area)}} \tag{13.11}\]

When the rate is normalized per catalyst particle volume it is convenient to define \(\epsilon\) as the catalyst bed void fraction, Equation 13.12. It is simply the fraction of the bed volume that is not occupied by catalyst particles. Using that definition, an expression for ratio of the particle volume to the bed volume can be generated, Equation 13.13. The rate per particle volume then can be renormalized by multiplying it by this ratio, Equation 13.14.

\[ \epsilon = \frac{V_{void}}{V_{bed}} = \frac{V_{void}}{V_{void} + V_{part}} \tag{13.12}\]

\[ \frac{V_{part}}{V_{bed}} = \frac{V_{bed} - V_{void}}{V_{bed}} = \frac{1 - \frac{V_{void}}{V_{bed}}}{1} = 1 - \epsilon \tag{13.13}\]

\[ r_{\text{(per reactor volume)}} = \left( 1 - \epsilon \right) r_{\text{(per particle volume)}} \tag{13.14}\]

13.6.3 Concentration and Temperature Gradients in Packed Bed PFRs

The renormalizations described above all make the implicit assumption that the fluid composition and temperature is uniform in any reactor cross-section. As illustrated Figure 13.5, gradients can form at the interface between two phases, and if one of the phases is porous, gradients can also form within the pores. The middle of the figure shows a cross-section of a packed bed PFR and then zooms in at the bottom of the figure to just show portions of two porous catalyst particles in gray and the fluid in blue. The zoomed in view on the left side shows a uniform blue in the space between the catalyst particles and within the pores of the portions of the two particles that are visible. The uniformity of the blue means that the concentration and temperature are uniformly the same everywhere. This is what the renormalizations assume.

Figure 13.5: Concentration and temperature gradients between the bulk of the fluid in the void space and the surface of the catalyst particles and within the catalyst particles.

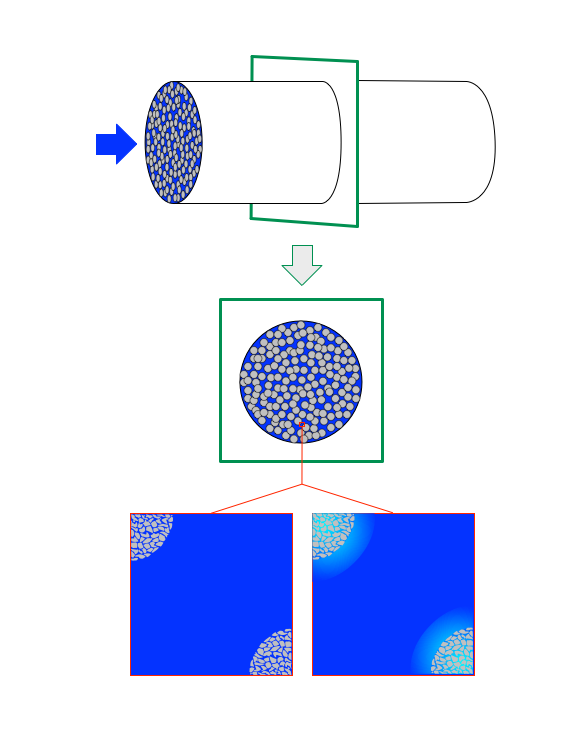
The zoomed in view shown in the lower right of the figure shows that in fact, there can be temperature and concentration gradient between the bulk of the fluid and the external surface of the catalyst particles and there can be concentration and temperature gradients within the pores of the solid catalyst particles. The blue color in the bulk of the fluid (center of the zoomed view) is uniform, but a gradient in color (representative of concentration and temperture gradients) is seen as the external surface of the two particles are approached. Concentration and temperature gradients between the bulk of the fluid and the surface of the particles are referred to as external gradients. Looking more closely at the figure it can be seen that there is also a gradient within the catalyst particles. These gradients are called internal gradients.

The problem this presents is as follows. The concentrations and temperatures that are used in the rate expression and the reactor design equations are the bulk fluid concentrations and temperatures. If there are no gradients, as in the lower left of the figure, this does not cause a problem. However, if there are gradients, then the concentrations and temperature within the catalst particle are different from those in the bulk fluid. In other words, the rate should be calculated using the concentrations and temperatured within the catalyst pores because that is where the reaction is taking place, but instead, the rate is being calculated using the bulk fluid concentrations and temperature.

The consequences of using the bulk fluid reactant concentrations in the rate expression when there are gradients present is indicated in Figure 13.6. The upper panel, a in the figure, represents a situation where the catalyst (gray) is not porous, but there are gradients (pink) between the bulk fluid (blue) and the catalyst surface. The region within which the gradients exist (pink) is called the boundary layer. The graph on the right of the top panel plots the concentration of a reactant as a function of the distance into the boundary layer. The concentration of a reactant decreases across the boundary layer. As a consequence, the concentration at the surface of the catalyst, \(C_{surf}\), is smaller than the bulk fluid concentration \(C_{bulk}\). It is important to realize that no reaction occurs within the boundary layer because the reaction is catalyzed and only occurs on the catalyst surface. The net effect of the external gradient is that the concentration that should be used in the rate expression, \(C_{surf}\), is smaller than the bulk fluid concentration \(C_{bulk}\). \(C_{surf}\) is colored red in the graph to indicate that reaction takes place at that concentration. If the gradient is ignored and the rate is calculated using the bulk concentration, the rate will be larger than it should be, and the predictions made by the reactor design equaions will be incorrect.

Figure 13.6: The effect of external gradients, internal gradients and both external and internal gradients in concentration upon the rate of reaction. The concentrations at the location were reaction occurs are indicated in red in the graphs.

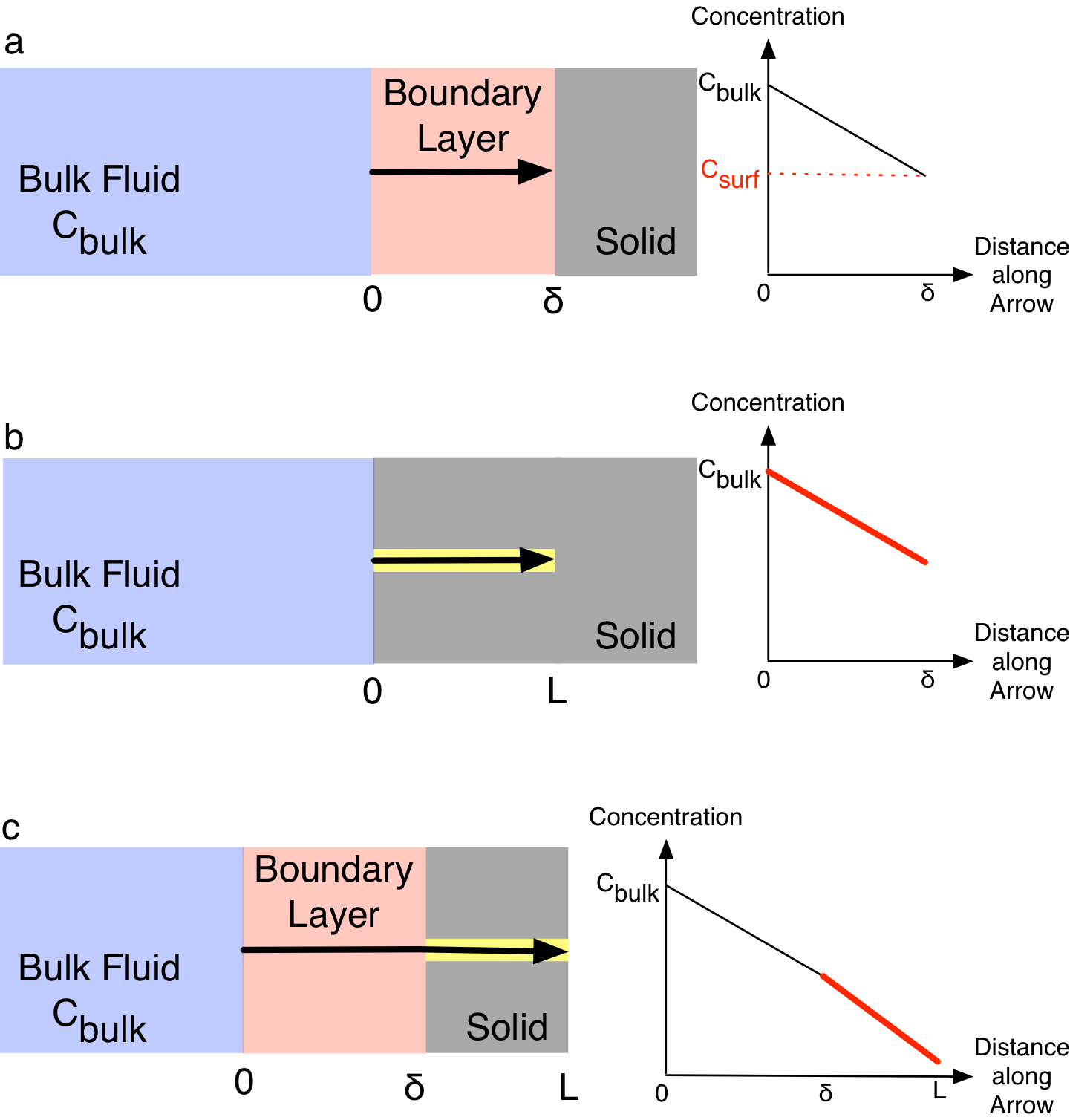
The middle panel, b in Figure 13.6, depicts a situation where there are no external gradients, but the catalyst is porous and the reactant diffuses into a catalyst pore (yellow). Since there isn’t a boundary layer, the concentraton at the external surface of the catalyst is equal to \(C_{bulk}\). Being within the pore (and therefore in contact with the catalyst surface), some of the reactant can react as it diffuses into the catalyst pore. The graph to the right of that schematic plots the reactant concentration as a function of the distance into the catalyst particle. The line in the graph is colored red because reaction takes place all along the pore. In other words, the rate should not be evaluated only at \(C_{bilk}\), but at a range of concentrations that exist within the catalyst pore. Once again, if the rate is evaluated only at \(C_{bulk}\) it will be too large and the results from the reactor design equations will be incorrect.

Without going into as much detail, the bottom panel, c in Figure 13.6, depicts a situation where there are both external and internal gradients. The graph to the right of the schematic shows that in this situation the rate again occurs over a range of reactant concentrations, but all of them are less than the bulk fluid concentration. Yet again, if the rate is evaluated only at \(C_{bulk}\) it will be too large and the results from the reactor design equations will be incorrect.

Several approaches are possible to account for concentration and temperature gradients associated with heterogeneous catalysts. This chapter does not attempt to present a comprehensive discussion of the topic, but instead considers one of the simplest of situations, illustrating one approach to accounting for concentration gradients. In particular, this chapter only considers concentration gradients (an analogous approach can be used to account for temperature gradients), it only considers a system where Fick’s law describes diffusion and where there is equal and opposite counter-diffusion. Additional limitations will be introduced during the analyses. In short, this chapter is intended to provide an introductory basis for those who wish to learn more through independent study or a second course on reaction engineering.

Accounting for External Concentration Gradients The flux of a reactant, A, through the boundary layer is usually described in terms of a mass transfer coefficient, \(k_c\), where the subscript “c” denotes that the mass transfer coefficient is for use with concentrations as expressed in Equation 13.15. The mass transfer coefficient will depend upon the geometry of the system under consideration, the fluid flow rate and fluid properties. As a consequence, values for mass transfer coefficients are often found from dimensionless correlations. Equation 13.16 is an example of such a correlation for the dimensionless quantity, \(j_D\), in terms of the Reynolds number, \(N_{Re}\). Equations 13.17 and 13.18 are the defining equations for \(j_D\) and \(N_{Re}\). Equations 13.15 through 13.18 apply specifically to flow through a packed bed of spherical particles with Reynolds numbers greater than 50. A number of correlations of this type are available; a good mass transfer textbook or chemical engineering handbook should be consulted to find an appropriate correlation for other conditions. Both \(j_D\) and \(N_{Re}\) may be defined differently, depending on the specific correlation being used.

\[ N_A = k_c\left( C_{A,bulk} - C_{A,surf} \right) \tag{13.15}\]

\[ j_D = 0.61N_{Re}^{-0.41} \tag{13.16}\]

\[ j_D = \frac{\pi D_{tube}^2k_c}{4\dot{V}}\left(\frac{\mu}{\rho D_A} \right)^{2/3} \tag{13.17}\]

\[ N_{Re} = \frac{2\dot{V}\rho}{3\pi D_{tube}^2 \mu \left(1-\epsilon \right)D_{part}} \tag{13.18}\]

In general, the concentration of the reactant at the external surface of the catalyst particle is not known. Suppose, however, that the catalyst was not porous as in panel a of Figure 13.6, and that the system had reached steady state. At steady state, the flux given by Equation 13.15 must just equal the rate of reaction on the surface of the catalyst particle. If this weren’t true, reactant would accumulate at the surface, and accumulation does not occur at steady state. Note that the rate expression should be evaluated at \(C_{A,surf}\), not \(C_{A,bulk}\). Then, for a steady state system, the flux according to Equation 13.15 can be set equal to the rate predicted by the rate expression at \(C_{A,surf}\) (assuming the rate expression has been normalized per unit catalyst surface area).

The resulting expression can be solved to find the concentration of A at the surface. For example, if the reaction rate is first order in A, this leads to Equation 13.19 for the surface concentration of A. Substitution of Equation 13.19 back into the first order rate expression leads to a rate expression in terms of the bulk fluid concentration of A, Equation 13.20. The rate expression in terms of the bulk fluid concentration still has the appearance of a first order rate expression, Equation 13.21, but the apparent rate coefficient, \(k^{\prime}\), is no longer a simple rate coefficient, Equation 13.22. Thus, if only external concentration gradients were present and the catalyst was non-porous, the rate expression in Equation 13.20 could be used in an ideal reactor model, and the model would correctly account for the external concentration gradient. This analysis only applies if the reaction is first order and the catalyst is non-porous.

\[ C_{A,surf} = \frac{k_c}{k + k_c}C_{A,bulk} \tag{13.19}\]

\[ -r_A = \frac{k k_c}{k + k_c}C_{A,bulk} = \left( \frac{1}{k} + \frac{1}{k_c} \right)^{-1}C_{A,bulk} \tag{13.20}\]

\[ -r_A = k^{\prime}C_{A,bulk} \tag{13.21}\]

\[ \frac{1}{k^{\prime}} = \frac{1}{k} + \frac{1}{k_c} \tag{13.22}\]

Accounting for Internal Concentration Gradients Accounting for internal concentration gradients associated with heterogeneous catalysts requires some sort of model for the pore structure of the catalyst. Each catalyst particle is likely to have its own unique pore structure. As a result, it is not practical to attempt to construct an exact physical model for the pore structure. Instead, common approaches are to construct a network of pores that are interconnected at nodes where a specified number of pores meet or to assume straight pores with circular cross sections and a distribution of pore diameters. An even simpler approach, that will be used here, is to adopt a pseudo-continuum pore model.

Figure 13.7: In the pseudo-continuum pore model, the reagents are assumed to diffuse in the radial direction as indicated by the arrows.

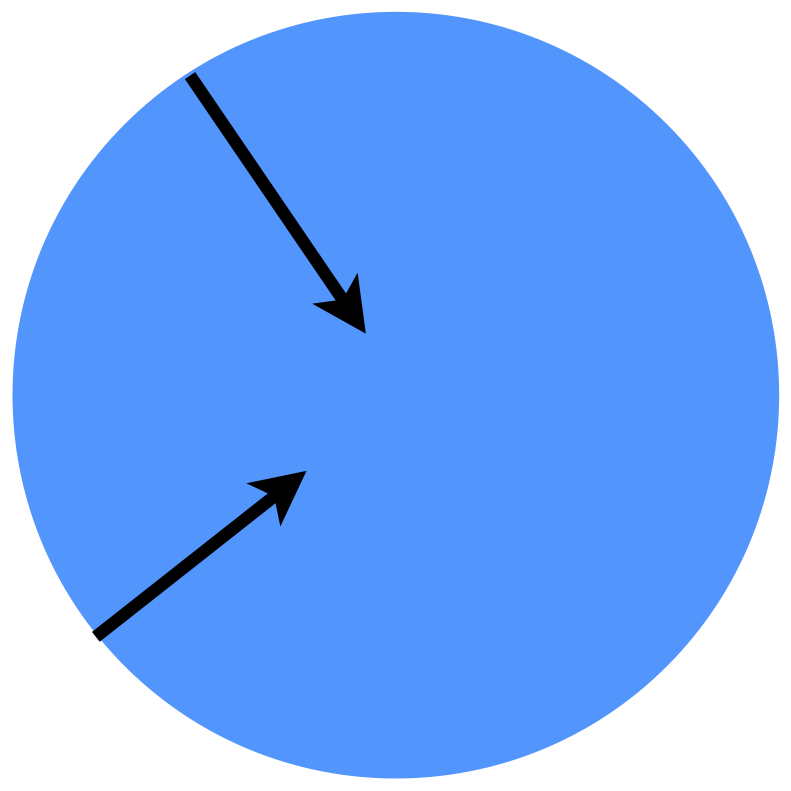
The pseudo-continuum pore model completely ignores the pore structure of the solid. Instead, it treats the catalyst particle as if it is a single homogeneous phase. It further assumes that the reactants diffuse in a straight line in the radial direction, as shown in Figure 13.7. Here, the diffusion process is assumed to obey Fick’s law, but an effective diffusivity is used in place of the true diffusion coefficient. With that, a steady state mole balance on reactant A within a spherical catalyst particle takes the form given in Equation 13.23. It should be noted, in particular, that the appropriate diffusion coefficient to use when modeling a porous solid depends upon the chemical species present, the nominal diameter of the catalyst pores and the mode of diffusion. Possible modes of diffusion include ordinary molecular diffusion, Knudsen diffusion, configurational diffusion and surface diffusion.

\[ -D_{eff,A}\left( \frac{\partial^2 C_A}{\partial r^2} + \frac{2}{r} \frac{\partial C_A}{\partial r}\right) = r_A \tag{13.23}\]

In reality, of course, if you looked at any spherical shell within the catalyst particle, only a fraction of the surface of that shell would be available for diffusion because the reactant could not really diffuse through the solid, only the pores. It is commonly assumed that the fraction of the surface of any spherical shell that is available for diffusion is equal to the void fraction, \(\varepsilon\), of the catalyst particle (not the void fraction of the packed bed of particles, \(\epsilon\)). Similarly, the actual path followed by a diffusing reactant in reality will twist and turn so that the distance the reactant travels to reach the center of the particle is greater than the radius of the particle. A quantity known as the tortuosity, \(\tau\), is used to account for the difference between the straight line distance to the center and the actual path length. With these two correction factors, the effective diffusivity can be related to the appropriate true diffusion coefficient for species A according to Equation 13.24.

\[ D_{eff,A} = \frac{\varepsilon D_A}{\tau} \tag{13.24}\]

Assuming the total number of moles is not changed by reaction, a mole balance can be written for reactant A on a differentially thin spherical shell within the spherical catalyst particle. Assuming that the rate is again first order, but it is normalized per unit mass of catalyst, and letting \(\rho_{part}\) represent the apparent density of a catalyst particle, Equation 13.25 results by taking the limit as the shell thickness goes to zero. Equation 13.25 is equivalent to Equation 13.23; it is a second order differential equation that can be integrated analytically to obtain an expression for the concentration of A as a function of radial position within the catalyst particle. Doing so leads to two constants of integration. The values of these constants of integration are found by applying the boundary conditions specified in Equations 13.26 and 13.27. The first boundary condition simply requires that the concentration of A at the entrance to the porous solid is equal to the external surface concentration of A. The second boundary condition is a symmetry condition that requires that the concentration gradient go to zero at the center of the particle.

\[ D_{eff,A} \frac{1}{r^2} \frac{d}{dr}\left( r^2 \frac{dC_A}{dr} \right) = \rho_{part}k C_A \tag{13.25}\]

\[ C_A \big\vert_{r=R_{part}} = C_{A,surf} \tag{13.26}\]

\[ \frac{dC_A}{dr} \Big \vert_{r=0} = 0 \tag{13.27}\]

Integrating Equation 13.25, finding the constants of integration and substituting them back into the result leads to Equation 13.28 for the concentration of A as a function of radial position within the catalyst particle. Equation 13.28 only applies for a spherical catalyst particle with a first order reaction taking place. E. W. Thiele was among the first to derive models of this kind, and consequently the name Thiele modulus is given to the dimensionless quantity \(\phi\), Equation 13.29, which represents the ratio of reaction rate to diffusion rate. It should be noted that in general, the definition of the Thiele modulus depends upon the geometry of the catalyst particle and the form of the rate expression.

\[ C_A\left(r\right) = C_{A,surf} \frac{\sinh{\left(\phi \frac{r}{R_{part}}\right)}}{\frac{r}{R_{part}}\sinh{\phi}} \tag{13.28}\]

\[ \phi = R_{part}\sqrt{\frac{k\rho_{part}}{D_{eff,A}}} \tag{13.29}\]

The flux of reactant A into the catalyst through its surface (i. e. in the negative \(r\) direction) is related to the gradient in the concentration of A at the surface according to Equation 13.30. Substitution of the derivative of Equation 13.28 into equation Equation 13.30 gives an expression for the flux of A into the catalyst particle, Equation 13.31. Multiplication of this flux by the external surface area of the catalyst particle gives the rate at which reactant A enters the particle.

\[ -N_A = D_{eff,A} \left( \frac{dC_A}{dr}\Big\vert_{r = R_{part}} \right) \tag{13.30}\]

\[ -N_A = \frac{\phi D_{eff,A} C_{A,surf}}{R_{part}} \left( \frac{1}{\tanh{\phi}} - \frac{1}{\phi} \right) \tag{13.31}\]

As before, at steady state, the rate at which A enters the catalyst particle must just equal the rate of reaction of A within the particle, because otherwise A would accumulate within the particle. It is interesting to compare the rate of reaction given above to the what the rate would equal if there were no concentration gradients. Letting \(\eta\) represent the ratio of the actual rate of reaction (where concentration gradients exist) to the rate that would be observed if there were no concentration gradients (and \(C_A = C_{A,surf}\) everywhere within the catalyst particle) leads to Equation 13.32. This quantity is known as the effectiveness factor; its value is given by Equation 13.32 only when the reaction is first order and the catalyst particles are spherical.

\[ \eta = \frac{3}{\phi} \left( \frac{1}{\tanh{\phi}} - \frac{1}{\phi} \right) \tag{13.32}\]

The utility of the effectiveness factor can be understood by first considering a situation where the external concentration gradients are negligible, such as that depicted in panel b of Figure 13.6. That is, consider the case where the concentration gradient across the boundary layer is negligible. In this case, \(C_{A,surf} = C_{A,bulk}\) and the actual rate of reaction, including the effect of the concentration gradients within the pores, is simply equal to the rate of reaction given by the rate expression for the bulk fluid concentration multiplied by the effectiveness factor. Put differently, in the absence of concentration gradients in the boundary layer, all that is needed in order to correct one of the ideal reactor models so that it accounts for the concentration gradients within the spherical catalyst particles is to multiply the rate expression by the effectiveness factor, as in Equation 13.33, where the rate would be normalized per unit catalyst volume.

\[ -r_A = \eta \rho_{part}kC_{A,bulk} \tag{13.33}\]

Figure 13.8 plots the effectiveness factor for a first order reaction taking place in a spherical catalyst particle as a function of the Thiele modulus. The figure shows that as the Thiele modulus goes to zero, the effectiveness factor approaches one. The effectiveness factor remains close to one for values of the Thiele modulus up to ca. 1, so generally one would prefer to operate a reactor at a Thiele modulus around 1 or less. At values of the Thiele modulus greater than 1, the effectiveness factor decreases rapidly, eventually approaching an asymptotic slope equal to \(\frac{3}{\phi}\) (for a first-order reaction in a spherical particle).

Figure 13.8: Effectiveness factor for a first order reaction in a spherical catalyst particle.

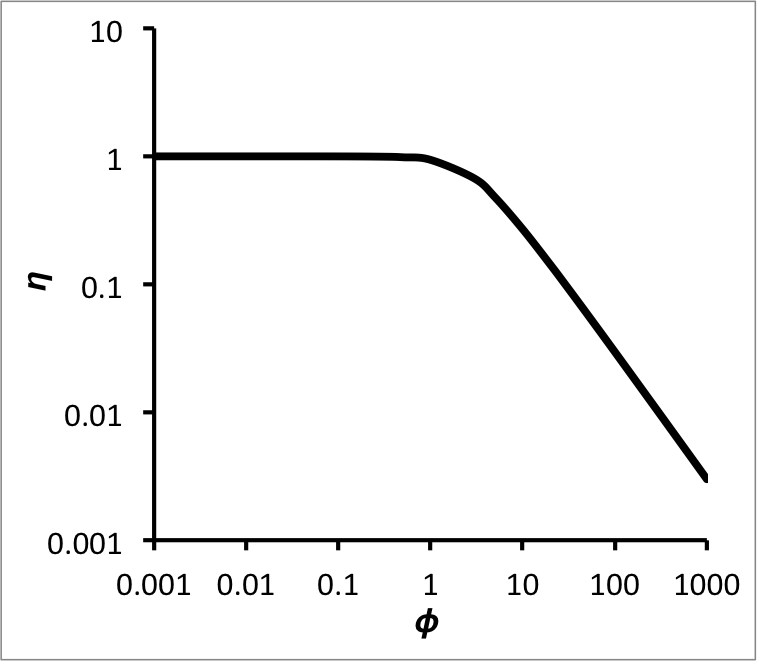
A word of caution is in order. When the reaction is first order, as in the analysis presented above, the Thiele modulus does not depend upon the concentration of A at the catalyst surface. This is rarely the case; for other reaction orders, the corresponding Thiele modulus, and consequently the effectiveness factor, depends upon the concentration of A at the catalyst surface. This means that as the reaction proceeds, the effectiveness factor will change. In addition, for a spherical catalyst particle and most reaction orders other than one, it has not proven possible to obtain an analytical expression for the effectiveness factor like Equation 13.32, which is for a first order reaction. Instead, the effectiveness factor must be calculated numerically. Thus, it is possible to construct a plot of the effectiveness factor as a function of the Thiele modulus, similar to Figure 38.3. The problem, however, is that when that effectiveness factor is substituted into the PFR design equation, as in Equation 13.33, it is no longer a constant. A rigorous solution of Equation 13.33 requires that the variation in the effectiveness factor be accounted for.

Accounting for Simulaneuous External and Internal Gradients Returning to the first order case, if the concentration gradient across the boundary layer is significant, as in panel c of Figure 13.6, Equation 13.31 is still valid. The only problem is that \(C_{A,surf}\) is no longer equal to \(C_{A,bulk}\). However, for a steady state process, the flux into the catalyst must just equal the flux through the boundary layer. This is expressed in Equation 13.34 which can be solved for \(C_{A,surf}\) giving Equation 13.35, and the result can be substituted back into Equation 13.31 to get an expression for the flux of reactant A into the catalyst in terms of the bulk fluid concentration of A, Equation 13.36. From that, an expression for the global effectiveness factor, \(\eta_G\), can be derived, Equation 13.37. The global effectiveness factor in Equation 13.37 is the actual rate of reaction (i. e. in the presence of concentration gradients in both the boundary layer and the pores) divided by the rate of reaction in the absence of concentration gradients (i. e. if \(C_A = C_{A,bulk}\) everywhere). Equation 13.37 only applies for a first order reaction taking place isothermally in a spherical catalyst particle.

\[ \frac{\phi D_{eff,A} C_{A,surf}}{R_{part}} \left( \frac{1}{\tanh{\phi}} - \frac{1}{\phi} \right) = k_c \left( C_{A,bulk} - C_{A,surf} \right) \tag{13.34}\]

\[ C_{A,surf} = \frac{\gamma C_{A,bulk} \tanh{\phi}}{\phi + \left( \gamma - 1 \right)\tanh{\phi}}\, \qquad \gamma = \frac{k_c R_{part}}{D_{eff,A}} \tag{13.35}\]

\[ -N_A = \frac{\gamma C_{A,bulk} D_{eff,A}}{R_{part}} \frac{\phi - \tanh{\phi}}{\phi + \left( \gamma - 1 \right) \tanh{\phi}} \tag{13.36}\]

\[ \eta_G = \frac{3}{\phi} \left( \frac{1}{\tanh{\phi}} - \frac{1}{\phi} \right) \frac{\gamma \tanh{\phi}}{\phi + \left( \gamma - 1 \right) \tanh{\phi}} \tag{13.37}\]

Once again, the approach presented in this unit is but one of many means of accounting for concentration gradients during heterogeneous catalysis. A similar approach can be applied to additionally account for temperature gradients. The approach used here uses the pseudo-continuum model for the porous solid; models can also be developed using other pore models. This approach can be adapted to catalyst geometries other than spherical and to situations where the total number of moles changes upon reaction. These topics are typically treated in much greater detail in advanced courses on kinetics and reaction engineering.

13.7 Examples

This chapter includes six examples of the analysis of an isolated PFR. The first three examples illustrate response tasks involving steady-state PFRs. A gas-phase reaction with negligible pressure drop is considered in Example 13.7.1, and a liquid-phase system in Example 13.7.2. In the former example, the reactor design equations are solved to find the PFR output, while in the latter they are solved to find the feed temperature in addition to the reactor output. Example 13.7.3 examines a gas-phase, packed-bed PFR where a momentum balance is used to account for pressure drop. Example 13.7.4 illustrates an optimization task for a gas-phase reaction with negligible pressure drop. Example 13.7.5 analyzes the start-up of the PFR from Example 13.7.2 where the transient takes the form of a front that propgates along the length of the reactor. Finally, a packed-bed PFR with concentration gradients within the catalyst pores is considered in Example 13.7.6.

13.7.1 Steady-State Conversion in a Gas-Phase PFR

The heat of reaction (1) is 44.8 kJ mol^-1, and the reaction is irreversible. The rate expression is equation (2) where the pre-exponential factor is 7.22 x 10⁶ mol atm^-2 cm^-3 s^-1 and the activation energy is 84.1 kJ mol^-1. A 10 foot long tubular reactor with a diameter of 1 inch is heated by a vapor condensing at 200 °C on the outside of the tube wall. The overall heat transfer coefficient is 7.48 x 10⁴ J h^-1 ft^-2 K^-1. Pressure drop through the reactor is negligible. If a gas phase mixture of 60% A and 40% B enters the reactor at 282 L min^-1, 2.5 atm and 175 °C and if the heat capacities of A, B and Z are equal to 18.0, 12.25 and 21.2 cal mol^-1 K^-1, what steady state outlet temperature and conversion of B will result?

\[ A + B \rightarrow Z \tag{1} \]

\[ r_1 = k_1 P_A P_B \tag{2} \]

---

Click Here to See What an Expert Might be Thinking at this Point

This assignment describes an isolated PFR and the manner in which it operates and asks questions about the reactor outputs. I will need to create a model for the reactor and use it to answer the questions. I’ll first summarize the assignment by assigning an appropriate variable symbol to each quantity provided in the narrative. I’ll use a subscripted “in” to denote values at the inlet to the reactor, a subscripted “out” to denote values at the reactor outlet, and I’ll add values for the ideal gas constant since I know I’ll need them. The assignment explicitly asks for the steady-state values of the quantities of interest, and from reading the assignment, I see that the PFR is neither isothermal nor adiabatic, but instead it is heated.

13.7.1.1 Assignment Summary

Given and Known Constants: \(\Delta H_1\) = 44.8 kJ mol^-1, \(k_{0,1}\) = 7.22 x 10⁶ mol atm^-2 cm^-3 s^-1, \(E_1\) = 84.1 kJ mol^-1, \(L\) = 10 ft, \(D\) = 1 in, \(T_{ex}\) = 200 °C, \(U\) = 7.48 x 10⁴ J h^-1 ft^-2 K^-1, \(y_{A,in}\) = 0.60, \(y_{B,in}\) = 0.40, \(\dot{V}_{in}\) = 282 L min^-1, \(P\) = 2.5 atm, \(T_{in}\) = 175 °C, \(\hat{C}_{p,A}\) = 18.0 cal mol^-1 K^-1, \(\hat{C}_{p,B}\) = 12.25 cal mol^-1 K^-1, \(\hat{C}_{p,Z}\) = 21.2 cal mol^-1 K^-1, and \(R\) = 8.314 J mol^-1 K^-1 = 0.08206 L atm mol^-1 K^-1.

Reactor System: Heated, steady-state PFR with negligible pressure drop

Quantities of Interest: \(T_{out}\) and \(f_B\)

13.7.1.2 Mathematical Formulation of the Solution

Click Here to See What an Expert Might be Thinking at this Point

I need to generate the reactor design equations for modeling this particular PFR as discussed in Chapter 6. The minimum number of mole balances is equal to the number of mathematically independent reactions plus one mole balance per inert species. Since I’m going to solve them numerically, it’s just as easy to write a mole balance on every reagent in the system (A, B, and Z in this assignment). The PFR operates at steady-state, so I’ll start with the general form of the steady-state PFR mole balance given in Equation 6.39. There is only one reaction taking place, so the summation reduces to a single term.

\[ \frac{d \dot{n}_i}{d z} =\frac{\pi D^2}{4}\cancelto{\nu_{i,1}r_1}{\sum_j \nu_{i,j}r_j} \]

This reactor is not isothermal, so the mole balances cannot be solved separately from an energy balance on the reacting gas. To generate that equation, I’ll start from the general form of the steady-state PFR energy balance, Equation 6.40. There are three reagents present in the reactor, so the first summation expands to three terms. Again, there is only one reaction taking place, so the final summation reduces to a single term. Knowing that I will be solving the design equations numerically, and that I’ll have to evaluate each of the derivatives, I’ll rearrange the equation into the form of a derivative expression (Appendix K).

\[ \cancelto{\left( \dot{n}_A \hat{C}_{p,A} + \dot{n}_B \hat{C}_{p,B} + \dot{n}_Z \hat{C}_{p,Z} \right)}{\left(\sum_i \dot{n}_i \hat{C}_{p,i} \right)} \frac{d T}{d z} = \pi D U\left( T_{ex} - T \right) - \frac{\pi D^2}{4}\cancelto{r_1 \Delta H_1}{\sum_j r_j \Delta H_j} \]

\[ \frac{d T}{d z} = \frac{\pi D U\left( T_{ex} - T \right) - \frac{\pi D^2}{4}r_1 \Delta H_1}{\dot{n}_A \hat{C}_{p,A} + \dot{n}_B \hat{C}_{p,B} + \dot{n}_Z \hat{C}_{p,Z}} \]

The PFR is being heated using the latent heat of a heat exchange fluid. Because only the latent heat is involved, the temperature of the exchange fluid is constant. That means that I can solve the combined mole and reacting fluid energy balances independently of an energy balance on the heat exchange fluid. (In this assignment I’m not provide with sufficient information to solve the exchange fluid energy balance, but neither does the assignment ask for anything that would need to be calculated using it.)

Finally, for PFRs a momentum balance is needed to account for pressure drop along the length of the reactor. In this assignment, however, it is noted that pressure drop is negligible, so I won’t add a momentum balance to the reactor design equations.

Reactor Design Equations

Mole balance design equations for A, B, and Z are presented in equations (3) - (5). The energy balance on the reacting gas is given in equation (6).

\[ \frac{d \dot{n}_A}{dz} = -\frac{\pi D^2}{4}r_1 \tag{3} \]

\[ \frac{d \dot{n}_B}{dz} = -\frac{\pi D^2}{4}r_1 \tag{4} \]

\[ \frac{d \dot{n}_Z}{dz} = \frac{\pi D^2}{4}r_1 \tag{5} \]

\[ \frac{d T}{d z} = \frac{\pi D U\left( T_{ex} - T \right) - \frac{\pi D^2}{4}r_1 \Delta H_1}{\left( \dot{n}_A \hat{C}_{p,A} + \dot{n}_B \hat{C}_{p,B} + \dot{n}_Z \hat{C}_{p,Z} \right)} \tag{6} \]

Click Here to See What an Expert Might be Thinking at this Point

The reactor design equations consist of four IVODEs and they contain four dependent variables, \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Z\), and \(T\), so there isn’t a need to either eliminate a dependent variable or add an IVODE. However, in order to solve the design equations numerically, initial values and a stopping criterion are needed.

I can define \(z=0\) to be the inlet to the reactor. The other initial values are then simply the values of the depedent variables at the reactor inlet. The length of the reactor is provided, so that can serve as the stopping criterion.

Initial Values and Stopping Criterion

Table 13.1: Initial values and stopping criterion for solving equations, (numbers).

Variable	Initial Value	Stopping Criterion
\(z\)	\(0\)	\(L\)
\(\dot{n}_A\)	\(\dot{n}_{A,in}\)
\(\dot{n}_B\)	\(\dot{n}_{B,in}\)
\(\dot{n}_Z\)	\(0\)
\(T\)	\(T_{in}\)

Click Here to See What an Expert Might be Thinking at this Point

In order to solve the IVODEs numerically I’ll need to do two things: calculate the values of the derivatives at the start of each integration step and calculate all of the initial and final values in Table 13.1.

At the start of each integration step, the independent variable (\(z\)) and the dependent variables (\(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Z\), and \(T\)) will be known, as will the given and known constants listed above. I will need to calculate any other quantities that appear in the derivatives expressions, equations (3) through (6).

Looking at those equations I see that I’ll need to calculate the rate, \(r_1\). I can use the rate expression, equation (2), to do that, but that wiill require me to calculate the rate coefficient, \(k_1\), and the partial pressures of A and B. The Arrhenius expression, Equation 4.8, can be used for the former and a defining equation for partial pressure for the latter.

\[ P_i = y_iP = \frac{\dot{n}_i}{\sum_i\dot{n}_i} \]

Ancillary Equations for Evaluating the Derivatives

\[ k_1 = k_{0,1} \exp{\left( \frac{-E_1}{RT} \right)} \tag{7} \]

\[ P_A = \frac{\dot{n}_A}{\dot{n}_A + \dot{n}_B + \dot{n}_Z}P \tag{8} \]

\[ P_B = \frac{\dot{n}_B}{\dot{n}_A + \dot{n}_B + \dot{n}_Z}P \tag{9} \]

Click Here to See What an Expert Might be Thinking at this Point

When I solve the IVODEs numerically, I’ll also need to calculate the initial and final values in Table 13.1. The reactor length and feed temperature are given in the assignment narrative. The narrative also provides the inlet mole fractions of A and B and the inlet volumetric flow rate. The ideal gas law can be used to calculate the total inlet molar flow rate which can be multiplied by each reagent mole fraction to calculate the inlet molar flow of that reagent.

\[ \dot{n}_{i,in} = y_{i,in} \dot{n}_{total,in} = y_{i,in} \frac{P\dot{V}_{in}}{RT_{in}} \]

Ancillary Equations for Calculating the Initial and Final Values

\[ \dot{n}_{A,in} = y_{A,in}\frac{P\dot{V}_{in}}{RT_{in}}\tag{10} \]

\[ \dot{n}_{B,in} = y_{B,in}\frac{P\dot{V}_{in}}{RT_{in}}\tag{11} \]

Click Here to See What an Expert Might be Thinking at this Point

At this point the reactor design equations can be solved numerically to get corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Z\), and \(T\) spanning the range from their initial (inlet) values to their final (outlet) values. The outlet temperature is one of the quantities of interest. The other, namely the fractional conversion of B can be calculated using its defining equation for an open system, Equation 3.5.

Ancillary Equations for Calculating the Quantities of Interest

Solving the reactor design equations yields \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Z\), and \(T\) as functions of \(z\) between 0 and \(L\). The outlet temperature and the conversion of B can be calculated using equations (12) and (13).

\[ T_{out} = T \big \vert_{z=L} \tag{12} \]

\[ f_B = \frac{\dot{n}_{B,in} - \dot{n}_B}{\dot{n}_{B,in}}\tag{13} \]

Calculations Summary

1. Substitute given and known constants into all equations.
2. When it is necessary to evaluate the derivatives
   1. \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Z\), and \(T\) will be available
   2. calculate \(k_1\), \(P_A\), and \(P_B\) using equtions (7) - (9).
   3. calculate \(r_1\) using equation (2).
   4. evaluate the derivatives using equations (3) - (6).
3. When it is necessary to calculate the initial and final values in Table 13.1
   1. \(T_{in}\) and \(L\) are known constants.
   2. calculate \(\dot{n}_{A,in}\) and \(\dot{n}_{B,in}\) using equations (10) and (11).
4. When it is necessary to calculate the quantities of interest, \(T \big\vert_{z=L}\) and \(f_B\)
   1. corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Z\), and \(T\), spanning the range from their initial values to their final values will be available.
   2. calculate %T_{out}$ and \(f_B\) using equations (12) and (13).

13.7.1.3 Numerical implementation of the Solution

1. Make the given and known constants available for use in all functions.
2. Write a derivatives function that
   1. receives the independent and dependent variables, \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Z\), and \(T\), as arguments,
   2. evaluates the derivatives as described in step 2 of the calculations summary, and returns them.
3. Write a reactor model function that
   1. calculates the initial and final values in Table 13.1 as described in step 3 of the calculations summary,
   2. gets corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Z\), and \(T\), spanning the range from their initial values to their final values by calling an IVODE solver and passing the following information to it
      1. the initial values and stopping criterion in Table 13.1 and
      2. the name of the derivatives function from step 2 above, c, checks that the solver successfully solved the IVODEs, and
   3. returns the values returned by the IVODE solver.
4. Perform the analysis by
   1. calling the reactor model function from step 3 above to get corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Z\), and \(T\), spanning the range from their initial values to their final values, and
   2. calculating the quantities of interest as described in step 4 of the calculations summary,

13.7.1.4 Results and Discussion

The calculations were performed as described above. The outlet temperature is 138 °C and the conversion of B is 81.6 %. Apparently the rate of heat transfer to the reactor from the vapor condensing on the outside of the reactor wall is less than the heat absorbed by the endothermic reaction. The feed enters at 175 °C, and despite the heat being supplied by the 200 °C heat exchange fluid, the reacting fluid temperature drops to 138 °C by the time it reaches the reactor outlet.

As the temperature drops, the reaction rate decreases. If heat was not being supplied, the temperature would have dropped even lower resulting in a lower conversion at the reactor outlet.

SCoRE Connection

Videos showing how to complete this assignment using either Matlab or Python, along with the Matlab and Python code, are available in SCoRE.

13.7.2 Required Steady-State PFR Feed Temperature

A perfectly insulated tubular reactor with a diameter of 10 cm and a length of 5 m is fed an aqueous solution containing A and B at concentrations of 1.0 and 1.2 M, respectively. This feed stream flows at 75 L min^-1. Reagents A and B react according to reaction (1) with a rate of reaction that is accurately described by equation (2). The rate coefficient displays Arrhenius temperature dependence with a pre-exponential factor equal to 8.72 x 10⁵ L mol^-1 min^-1 and an activation energy of 7200 cal mol^-1. The heat of reaction (1) is –10,700 cal mol^-1 and may be assumed to be constant. The heat capacity of the solution and the density of the solution may be taken to be constant and equal to those of water (1.0 cal g^-1 K^-1 and 1.0 g cm^-3). The pressure drop in the reactor is negligible. What feed temperature is needed in order to convert 95% of the A, and what will the outlet temperature be?

\[ A + B \rightarrow Y + Z \tag{1} \]

\[ r_1 = k_1 C_A C_B \tag{2} \]

---

Click Here to See What an Expert Might be Thinking at this Point

This assignment describes an isolated steady-state PFR and its operation, and it asks about reactor inputs and outputs. To begin, I’ll summarize the assignment by assigning appropriate variable symbols to all of the quantities it mentions. I’ll use a subscripted “in” to denote values that apply to the feed and a subscripted “out” to denote values that apply to the reactor outlet. I’ll add the ideal gas constant to the list since I know I’ll need it.

The assignment states that the reactor is perfectly insulated. That means that it does not exchange heat through its walls, i. e. it is adiabatic. The assignment does not explicitly state that it operates at steady-state, but there is no mention of a change in any of the reactor inputs anywhere in the narrative. If the reactor was operating in a transient mode, something would have had to change to initiate the transient. Since no such change is mentioned, I can safely assume steady-state operation.

13.7.2.1 Assignment Summary

Given and Known Constants: \(D\) = 10 cm, \(L\) = 5 m, \(C_{A,in}\) = 1.0 M, \(C_{B,in}\) = 1.2 M, \(\dot{V}_{in}\) = 75 L min^-1, \(k_{0.1}\) = 8.72 x 10⁵ L mol^-1 min^-1, \(E_1\) = 7200 cal mol^-1, \(\Delta H_1\) = –10,700 cal mol^-1, \(\tilde{C}_p\) = 1.0 cal g^-1 K^-1, \(\rho\) = 1.0 g cm^-3, \(f_A\) = 0.95, and \(R\) = 1.987 cal mol^-1 K^-1.

Reactor System: Adiabatic, steady-state PFR with negligible pressure drop

Quantities of Interest: \(T_{in}\) and \(T_{out}\)

13.7.2.2 Mathematical Formulation of the Solution

Click Here to See What an Expert Might be Thinking at this Point

In order to complete this assignment I will need to create a model of this PFR and use it to answer the questions posed. I need to generate the reactor design equations for this PFR in order to model it. The design equations always include mole balances. Knowing I’ll be solving the design equations numerically, I’ll just write a mole balance on every reagent present in the system. This reactor operates at steady-state, so the general form of the mole balance is given by Equation 6.39. There is only one reaction taking place, so the summation reduces to a single term.

\[ \frac{d \dot{n}_i}{d z} = \frac{\pi D^2}{4}\sum_j \nu_{i,j}r_j = \frac{\pi D^2}{4}\nu_{i,1}r_1 \]

The reactor is not isothermal, so I cannot solve the mole balances independently. I need to add an energy balance on the reacting fluid. The general form of the steady-state PFR reacting fluid energy balance is given by Equation 6.40. The narrative provides the gravimetric heat capacity and the density of the liquid phase reacting fluid, to the first term can be modified to use that information. This PFR is adiabatic, so the heat exchange term is equal to zero, and again, there is only one reaction taking place.

\[ \cancelto{\rho \dot{V} \breve{C}_p}{\left(\sum_i \dot{n}_i \hat{C}_{p,i} \right)} \frac{d T}{d z} = \cancelto{0}{\pi D U\left( T_{ex} - T \right)} - \frac{\pi D^2}{4}\cancelto{r_1 \Delta H_1}{\sum_j r_j \Delta H_j} \]

When I solve the design equations numerically, I’m going to need to evaluate the derivatives, so I will re-write the equation in the form of a derivative expression (see Appendix K).

\[ \frac{d T}{d z} = -\frac{\pi D^2}{4} \frac{r_1 \Delta H_1}{\rho \dot{V} \tilde{C}_p} \]

The reactor is adiabatic, so there isn’t a heat exchange fluid to write an energy balance on. The pressure drop is negligible, so a momentum balance is not needed.

Reactor Design Equations

Mole balance design equations for A, B, Y, and Z are presented in equations (3) through (6), and an energy balance on the reacting fluid is given in equation (7).

\[ \frac{d \dot{n}_A}{dz} = - \frac{\pi D^2}{4}r_1 \tag{3} \]

\[ \frac{d \dot{n}_B}{dz} = - \frac{\pi D^2}{4}r_1 \tag{4} \]

\[ \frac{d \dot{n}_Y}{dz} = \frac{\pi D^2}{4}r_1 \tag{5} \]

\[ \frac{d \dot{n}_Z}{dz} = \frac{\pi D^2}{4}r_1 \tag{6} \]

\[ \frac{d T}{d z} = -\frac{\pi D^2}{4} \frac{r_1 \Delta H_1}{\rho \dot{V} \tilde{C}_p} \tag{7} \]

Click Here to See What an Expert Might be Thinking at this Point

There are five IVODE reactor design equations and they contain five dependent variables (\(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and %T%), so there isn’t a need to eliminae a dependent variable or add an IVODE.

Initial values and a stopping criterion are needed when solving IVODEs numerically. I can define \(z=0\) to be the inlet to the reactor, in which case the other initial values are the molar flow rates and the temperture at the reactor inlet. The feed only contains A and B, so the inlet molar flow rates of Y and Z are zero. The length of the reactor is given, so that can serve as the stopping criterion.

Note

The assignment also specifies the conversion of A. As such, I could have used the final value of A \(\left(\dot{n}_{A,out} = \dot{n}_{A,in}\left( 1 - f_A \right)\right)\) as the stopping criterion. In that case I’d calculate \(T_{in}\) below using an implicit equation that requires the reactor length to equal \(L\) \(\left(T_{in}: z_{out} = L\right)\).

In the solution presented here I am using \(z=L\) as the stopping criterion and calculating \(T_{in}\) below using an implicit equation requires the conversion to have the specified value \(\left(T_{in}: f_{A} \big \vert_{z=L} = f_A\right)\).

Both approaches are valid and will produce the same results.

Initial Values and Stopping Criterion

Table 13.2: Initial values and stopping criterion for solving equations, (numbers).

Variable	Initial Value	Stopping Criterion
\(z\)	\(0\)	\(L\)
\(\dot{n}_A\)	\(\dot{n}_{A,in}\)
\(\dot{n}_B\)	\(\dot{n}_{B,in}\)
\(\dot{n}_Y\)	\(0\)
\(\dot{n}_Z\)	\(0\)
\(T\)	\(T_{in}\)

Click Here to See What an Expert Might be Thinking at this Point

In order to solve the IVODEs numerically I’ll need to do two things: calculate the values of the derivatives at the start of each integration step and calculate all of the initial and final values in Table 13.2. At the start of an integration step, the independent (\(z\)) and dependent variables (\(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\)) will be known, as will the given and known constants listed above. I will need to calculate any other quantities that appear in the derivatives expressions, equations (3) - (7).

In those equations, the reaction rate, \(r_1\), and the volumetric flow rate, \(\dot{V}\), are unknown. The rate can be calculated using the rate expression, equation (2). In order to do that, the rate coefficient and the concentrations of A and B must be calculated. The rate coefficient can be calculated using the Arrhenius expression, Equation 4.8. The concentrations can be calculated using the defining equation for concentration in an open system, Equation 1.15. The reacting fluid is a liquid; assuming it to be an incompressible ideal mixture means that the volumetric flow rate will be constant and equal to the inlet volumetric flow rate.

Ancillary Equations for Evaluating the Derivatives

\[ k_1 = k_{0,1} \exp{\left( \frac{-E_1}{RT} \right)} \tag{8} \]

\[ C_A = \frac{\dot{n}_A}{\dot{V}} \tag{9} \]

\[ C_B = \frac{\dot{n}_B}{\dot{V}} \tag{10} \]

\[ \dot{V} = \dot{V}_{in} \tag{11} \]

Click Here to See What an Expert Might be Thinking at this Point

When I solve the IVODEs numerically, I’ll also need to calculate the initial and final values in Table 13.2. The reactor length, \(L\), is provided in the assignment narrative, and the inlet molar flow rates of A and B can be calculated from their known inlet concentrations and the inlet volumetric flow rate, Equation 1.15.

The feed temperature, \(T_{in}\), is not specified. Indeed, it is one of the quatntities of interest. Instead, however, a second outlet value, namely the conversion, is provided. The inlet temperature must result in a conversion, \(f_A \big \vert_{z=L}\), equal to the specified conversion, \(f_A\), listed among the given and known quantities above. As described in Appendix K, this can be written as an implicit equation for calculating \(T_{in}: f_A \big \vert_{z=L} = f_{A,out}\). That implicit equation can be written as a residual expression (see Appendix J) and solved numerically.

\[ 0 = f_{A,out} - f_A \big \vert_{z=L} \]

\[ 0 = f_{A,out} - \frac{\dot{n}_{A,in} - \dot{n}_A \big\vert_{z=L}}{\dot{n}_{A,in}} \]

\[ 0 = \dot{n}_{A,in}f_{A,out} - \dot{n}_{A,in} + \dot{n}_A \big\vert_{z=L} \]

\[ 0 = \dot{n}_A \big \vert_{z=L} - \dot{n}_{A,in}\left( 1 - f_A \right) = \epsilon \]

Ancillary Equations for Calculating the Initial and Final Values

The inlet molar flow rates can be calculated using equations (12) and (13). The inlet temperature, \(T_{in}: f_A \big \vert_{z=L} = f_{A,out}\), can be found by numerically solving the implicit equation, (14), for its value.

\[ \dot{n}_{A,in} = \dot{V}_{in}C_{A,in} \tag{12} \]

\[ \dot{n}_{B,in} = \dot{V}_{in}C_{B,in} \tag{13} \]

\[ 0 = \dot{n}_A \big \vert_{z=L} - \dot{n}_{A,in}\left( 1 - f_A \right) = \epsilon \tag{14|} \]

Click Here to See What an Expert Might be Thinking at this Point

At this point the IVODEs can be solved for the feed temperature, \(T_{in}\), and corresponding set of values of \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\) that span the range from their initial values to their final values. There aren’t any other quantities of interest that need to be calculated.

Solving the reactor design equations yields \(T_{in}\), and corresponding set of values of \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\) that span the range from their initial (feed) values to their final (outlet) values. The quantities of interest are \(T_{in}\) and \(T_{out} = T \big \vert_{z=L}\).

Calculations Summary

1. Substitute given and known constants into all equations.
2. When it is necessary to evaluate the derivatives
   1. \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\) will be available.
   2. calculate \(k_1\) and \(\dot{V}\) using equations (8) and (11).
   3. calculate \(C_A\) and \(C_B\) using equations (9) and (10).
   4. calculate \(r_1\) using equation (2).
   5. evaluate the derivatives using equations (3) through (7).
3. When it is necessary to calculate the initial and final values other than \(T_in\) in Table 13.2
   1. \(L\) is a known constant.
   2. calculate \(\dot{n}_{A,in}\) and \(\dot{n}_{B,in}\) using equations (12) and (13).
4. When it is necessary to evaluate the residual, \(\epsilon\), corresponding to the implicit equation for \(T_in\), equation (14)
   1. a guess for \(T_in\) will be available for use in all equations.
   2. solve the IVODEs, equations (3) through (7), using that guess along with the other initial values and stopping criterion in Table 13.2 and get the value of \(\dot{n}_A \big \vert_{z=L}\).
   3. calculate \(\epsilon\) using equation (14).
5. When it is necessary to calculate the quantities of interest, \(T_{in}\) and \(T_{out}\)
   1. \(T_{in}\) and corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\), spanning the range from their initial (inlet) values to their final (outlet) values will be available.
   2. \(T_{out} = T \big \vert_{z=L}\)

13.7.2.3 Numerical implementation of the Solution

1. Make the given and known constants available for use in all functions.
2. Define a variable to hold \(T_{in}\) and make it available to all functions.
3. Write a derivatives function that
   1. receives the independent and dependent variables, \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\), as arguments,
   2. evaluates the derivatives as described in step 2 of the calculations summary, and returns them.
4. Write a residuals function that
   1. receives a guess for \(T_{in}\) and makes it available to all functions,
   2. evaluates \(\epsilon\) as described in step 4 of the calculations summary, and returns it.
5. Write a reactor model function that
   1. has access to \(T_in\),
   2. calculates the other initial and final values in Table 13.2 as described in step 3 of the calculations summary,
   3. gets corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\), spanning the range from their initial values to their final values by calling an IVODE solver and passing the following information to it
      1. the initial values and stopping criterion in Table 13.2 and
      2. the name of the derivatives function from step 3 above, d, checks that the solver successfully solved the IVODEs, and
   4. returns the values returned by the IVODE solver.
6. Perform the analysis by
   1. calculating \(T_{in}\) by calling an ATE solver using the following arguments
      1. an initial guess for \(T_{in}\) and
      2. the name of the residuals funtions from step 4
   2. calling the reactor model function from step 5 to get corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\), spanning the range from their initial (inlet) values to their final (outlet) values,
   3. calculating the quantities of interest as described in step 5 of the calculations summary.

13.7.2.4 Results and Discussion

The calculations were performed as described above. When the feed temperature is 46 °C, 95% of the A in the feed is converted and the outlet temperature is 56.2 °C. When an exothermic reaction occurs in an adiabatic reactor, the temperature is expected to rise. In this case the temperature only rises by 10 °C, so it was not necessary to cool the reacting fluid during processing.

SCoRE Connection

Videos showing how to complete this assignment using either Matlab or Python, along with the Matlab and Python code, are available in SCoRE.

13.7.3 Pressure Drop in a Steady-State, Gas-Phase PFR

The gas-phase decomposition of A according to reaction (1) takes place at steady-state in a PFR. The feed to the reactor is 75% A and 25% inert gas flowing at 100 cm³ s^-1 (0.44 g s^-1), 3 atm and 400 °C. The reactor diameter is 2.5 cm and its length is 8 m. It is surrounded by a shell containing a molten salt at a constant temperature of 375 °C. The heat transfer coefficient between the reactor and shell is 187 kJ h^-1 m^-2 K^-1. The reaction is catalytic, and the reactor is packed with catalyst particles with a 0.25 cm diameter, a sphericity of 0.7, and a bed porosity of 0.60. The rate expression for reaction (1) is given in equation (2) where \(k_{0,f}\) = 9.0 x 10¹⁷ mol cm³ s^-1 atm^-1, \(𝐸_𝑓\) = 285 kJ mol^-1, \(𝑘_{0,𝑟}\) = 4.09 x 10^-4 mol cm^-3 s^-1 atm^-4, and \(𝐸_𝑟\) = 85 kJ mol^-1. The heat of reaction is constant and equal to 200 kJ mol^-1. The heat capacities of the reagents are also constant: \(\hat{C}_{p,A}\) = 11.7 cal mol^-1 K^-1, \(\hat{C}_{p,Y}\) = 8.3 cal mol^-1 K^-1, \(\hat{C}_{p,Z}\) = 4.3 cal mol^-1 K^-1, and \(\hat{C}_{p,I}\) = 5.8 cal mol^-1 K^-1. The viscosity may be assumed to be constant and equal to 0.027 cP. What are the outlet temperature, pressure and conversion?

\[ A \leftrightarrows Y + 3 Z \tag{1} \]

\[ r_1 = k_fP_A - k_rP_YP_Z^3 \tag{2} \]

---

Click Here to See What an Expert Might be Thinking at this Point

To begin, I’ll summarize this assignment by assigning appropriate variable symbols to each quantity that is mentioned in the narrative. I’ll use a subscripted “in” to indicate values at the reactor inlet, a subscripted “out” to designate values at the outlet, a “p” to denote values associated with the catalyst particles, and I’ll add the gas constant since I know I’ll need it. I’ll use “I” to represent the inert gas present in the system. The assignment states that the PFR is heated and operates at steady-state.

13.7.3.1 Assignment Summary

Given and Known Constants: \(y_{A,in}\) = 0.75, \(y_{I,in}\) = 0.25, \(\dot{V}_{in}\) = 100 cm³ s^-1, \(\dot{m}_{in}\) = 0.44 g s^-1, \(P_{in}\) = 3 atm, \(T_{in}\) = 400 °C, \(D\) = 2.5 cm, \(L\) = 8 m, \(T_{ex}\) = 375 °C, \(U\) = 187 kJ h^-1 m^-2 K^-1, \(D_p\) = 0.25 cm, \(\Phi_s\) = 0.7, \(\varepsilon\) = 0.60, \(k_{0,f}\) = 9.0 x 10¹⁷ mol cm³ s^-1 atm^-1, \(𝐸_𝑓\) = 285 kJ mol^-1, \(𝑘_{0,𝑟}\) = 4.09 x 10^-4 mol cm^-3 s^-1 atm^-4, \(𝐸_𝑟\) = 85 kJ mol^-1, \(\Delta H_1\) = 200 kJ mol^-1, \(\hat{C}_{p,A}\) = 11.7 cal mol^-1 K^-1, \(\hat{C}_{p,Y}\) = 8.3 cal mol^-1 K^-1, \(\hat{C}_{p,Z}\) = 4.3 cal mol^-1 K^-1, and \(\hat{C}_{p,I}\) = 5.8 cal mol^-1 K^-1, \(\mu\) = 0.027 cP, and \(R\) = 8.314 J mol^-1 K^-1 = 82.06 cm³ atm mol^-1 K^1-.

Reactor System: heated, steady-state PFR

Quantities of Interest: \(T_{out}\), \(P_{out}\), and \(f_A\)

13.7.3.2 Mathematical Formulation of the Solution

Click Here to See What an Expert Might be Thinking at this Point

I need to generate the reactor design equations for modeling this particular PFR. The reactor design equations will be some combination of mole balances, an energy balance on the reacting fluid, an energy balance on the heat exchange fluid, and, since this is a PFR, a momentum balance. I prefer to write mole balances on every reagent (other than liquid solvents) in the system. The general steady-state form of the PFR mole balance is given in Equation 6.39. There is only one reaction, so the summation becomes one term.

\[ \frac{d \dot{n}_i}{d z} = \frac{\pi D^2}{4}\sum_j \nu_{i,j}r_j = \frac{\pi D^2}{4} \nu_{i,1}r_1 \]

The PFR is not isothermal, so I must add an energy balance on the reacting gas. Equation 6.40 presents the general, steady-state form of the energy balance. None of the terms in the equation can be eliminated, but the two summations can be expanded, and the equation can be rearranged into the form of a derivative expression (see Appendix K).

\[ \left(\sum_i \dot{n}_i \hat{C}_{p,i} \right) \frac{d T}{d z} = \pi D U\left( T_{ex} - T \right) - \frac{\pi D^2}{4}\sum_j r_j \Delta H_j \]

\[ \frac{d T}{d z} = \frac{\pi DU \left(T_{ex} - T\right)-{\frac{\pi D^2}{4}r_1 \Delta H_1}}{\dot{n}_A \hat{C}_{p,A} + \dot{n}_B \hat{C}_{p,I} + \dot{n}_Y \hat{C}_{p,Y} + \dot{n}_Z \hat{C}_{p,Z}} \]

There is a vapor that is exchanging its latent heat with the reacting gas. Because only latent heat is being exchanged, the temperature of the heat exchange fluid is constant. That temperature is known, so I can solve the mole and energy balances above independently of an energy balance on the exchange fluid. Furthermore, since the assignment does not ask anything about the exchange fluid, I won’t need to use an energy balance on the heat exchange fluid.

The assignment does not mention pressure drop, but it does provide all of the information needed for calculating it using the Ergun equation, Equation 6.42. More generally, in a real-world engineering assignment, I would not know wheter pressure drop will be significant or not, so I would want to calculate it.

\[ \frac{{dP}}{{dz}} = - \frac{{1 - \varepsilon }}{{{\varepsilon ^3}}}\frac{{{G^2}}}{{\rho {\Phi _s}{D_p}}}\left[ {\frac{{150\left( {1 - \varepsilon } \right)\mu }}{{{\Phi _s}{D_p}G}} + 1.75} \right] \]

Reactor Design Equations

Mole balance design equations for A, Y, Z, and I are presented in equations (3) through (6). An energy balance on the reacting gas is shown in equation (7), and a momentum balance on the gas is given in equation (8).

\[ \frac{d \dot{n}_A}{dz} = - \frac{\pi D^2}{4}r_1 \tag{3} \]

\[ \frac{d \dot{n}_Y}{dz} = \frac{\pi D^2}{4}r_1 \tag{4} \]

\[ \frac{d \dot{n}_Z}{dz} = 3\frac{\pi D^2}{4}r_1 \tag{5} \]

\[ \frac{d \dot{n}_I}{dz} = 0.0 \tag{6} \]

\[ \frac{d T}{d z} = \frac{\pi DU \left(T_{ex} - T\right)-{\frac{\pi D^2}{4}r_1 \Delta H_1}}{\dot{n}_A \hat{C}_{p,A} + \dot{n}_B \hat{C}_{p,I} + \dot{n}_Y \hat{C}_{p,Y} + \dot{n}_Z \hat{C}_{p,Z}} \tag{7} \]

\[ \frac{{dP}}{{dz}} = - \frac{{1 - \varepsilon }}{{{\varepsilon ^3}}}\frac{{{G^2}}}{{\rho {\Phi _s}{D_p}}}\left[ {\frac{{150\left( {1 - \varepsilon } \right)\mu }}{{{\Phi _s}{D_p}G}} + 1.75} \right] \tag{8} \]

Click Here to See What an Expert Might be Thinking at this Point

The reactor design equations are six IVODEs, and they contain six dependent variables (\(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), \(\dot{n}_I\), \(T\), and \(P\)), so it isn’t necessary to add an IVODE or eliminate a dependent variable. Initial values and a stopping criterion are needed in order to solve the IVODEs numerically. I can define \(z=0\) as the inlet to the reactor in which case the other initial values are simply the values of the dependent variables at the reactor inlet. Inlet mole fractions of A and I are specified, and the sum to one, so there isn’t any Y or Z in the feed. The reactor length is specified, so that can be used as the stopping criterion.

Initial Values and Stopping Criterion

Table 13.3: Initial values and stopping criterion for solving equations, (numbers).

Variable	Initial Value	Stopping Criterion
\(z\)	\(0\)	\(L\)
\(\dot{n}_A\)	\(\dot{n}_{A,in}\)
\(\dot{n}_Y\)	\(0\)
\(\dot{n}_Z\)	\(0\)
\(\dot{n}_I\)	\(\dot{n}_{I,in}\)
\(T\)	\(T_{in}\)
\(P\)	\(P_{in}\)

Click Here to See What an Expert Might be Thinking at this Point

In order to solve the IVODEs numerically I’ll need to do two things: calculate the values of the derivatives at the start of each integration step and calculate all of the initial and final values in Table 13.3. At the start of an integration step the independent and dependent variables (\(z\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), \(\dot{n}_I\), \(T\), and \(P\)) will be known along with the given and known constants listed in the assignment summary. I will need to calculate any other quantities that appear in the derivatives expressions, equations (3) through (8).

Examination of those equations reveals \(r_1\), \(G\) and \(\rho\) as unknowns that will need to be calculated. The rate expression, equation (2), can be used to calculate \(r_1\), but before that can be done, the two rate coefficients and the partial pressures of the reactants and products must be calculated. The rate coefficients can be calculated using the Arrhenius expression, Equation 4.8. The partial pressure of reagent \(i\) is simply its mole fraction times the total pressure.

\[ P_i = \frac{\dot{n}_i}{\sum_i \dot{n}_i}P = \frac{\dot{n}_i}{\dot{n}_A + \dot{n}_Y + \dot{n}_Z + \dot{n}_I}P \]

\(G\) can be calculated using its defining equation. The density could be calculated by multipying each molar flow rate times the corresponding molecular weight, to get mass flow rates of each reagent. These could then be totaled and divided by the volumetric flow rate to calculate the density. However, noting that the mass flow rate is constant (no nuclear reactions are taking place), the density can be calculated simply by dividing the mass flow rate by the volumetric flow rate.

\[ G = \frac{4\dot{m}_{in}}{\pi D^2} = \frac{4\dot{m}}{\pi D^2} \]

\[ \rho = \frac{\dot{m}_{in}}{\dot{V}} = \frac{\dot{m}P}{\left( \dot{n}_A + \dot{n}_Y + \dot{n}_Z + \dot{n}_I \right)RT} \]

Ancillary Equations for Evaluating the Derivatives

\[ k_{1,f} = k_{0,f} \exp{\left( \frac{-E_f}{RT} \right)} \tag{9} \]

\[ k_{1,r} = k_{0,r} \exp{\left( \frac{-E_r}{RT} \right)}\tag{10} \]

\[ P_A = \frac{\dot{n}_A}{\dot{n}_A + \dot{n}_Y + \dot{n}_Z + \dot{n}_I}P \tag{11} \]

\[ P_Y = \frac{\dot{n}_Y}{\dot{n}_A + \dot{n}_Y + \dot{n}_Z + \dot{n}_I}P \tag{12} \]

\[ P_Z = \frac{\dot{n}_Z}{\dot{n}_A + \dot{n}_Y + \dot{n}_Z + \dot{n}_I}P \tag{13} \]

\[ \dot{m} = \dot{m}_{in} \tag{14} \]

\[ G = \frac{4\dot{m}}{\pi D^2} \tag{15} \]

\[ \rho = \frac{\dot{m}P}{\left( \dot{n}_A + \dot{n}_Y + \dot{n}_Z + \dot{n}_I \right)RT} \tag{16} \]

Click Here to See What an Expert Might be Thinking at this Point

When I solve the IVODEs numerically, I’ll also need to calculate the initial and final values in Table 13.3. The inlet temperature and pressure and the reactor length are known constants. To calculate the inlet molar flow rates of A and I, the total molar flow rate can be calculated using the ideal gas law. Multiplying that by the mole fraction of a reagent will then give the molar flow rate of the reagent.

\[ \dot{n}_{i,in} = y_{i,in}\dot{n}_{total} = y_{i,in}\frac{P_{in}\dot{V}_{in}}{RT_{in}} \]

Ancillary Equations for Calculating the Initial and Final Values

\[ \dot{n}_{A,in} = y_{A,in}\frac{P_{in}\dot{V}_{in}}{RT_{in}} \tag{17} \]

\[ \dot{n}_{I,in} = y_{I,in}\frac{P_{in}\dot{V}_{in}}{RT_{in}} \tag{18} \]

Click Here to See What an Expert Might be Thinking at this Point

At this point the reactor design equations can be solved numerically to get corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), \(\dot{n}_I\), \(T\), and \(P\) spanning the range from their initial (inlet) values to their final (outlet) values. Thus, the outlet pressure and temperature are found by solving the IVODEs. The conversion can be calculated using its definition.

Ancillary Equations for Calculating the Quantities of Interest

Solving the reactor design equations yields sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), \(\dot{n}_I\), \(T\), and \(P\) spanning the range from their initial (inlet) values to their final (outlet) values. The outlet molar flow of A, temperature and pressure can be found using equations (19) - (21), after which the conversion can be calculated using equation (22).

\[ \dot{n}_{A,out} = \dot{n}_{A} \big \vert_{z=L} \tag{19} \]

\[ T_{out} = T \big \vert_{z=L} \tag{20} \]

\[ P_{out} = P \big \vert_{z=L} \tag{21} \]

\[ f_A = \frac{\dot{n}_{A,in} - \dot{n}_{A,out}}{\dot{n}_{A,in}} \tag{22} \]

Calculations Summary

1. Substitute given and known constants into all equations.
2. When it is necessary to evaluate the derivatives
   1. \(z\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), \(\dot{n}_I\), \(T\), and \(P\) will be available.
   2. calculate \(k_{0,f}\), \(k_{0,r}\), \(P_A\), \(P_Y\), \(P_Z\), and \(\dot{m}\) using equations (9) - (14).
   3. calculate \(r_1\), \(G\), and \(\rho\) using equations (2), (15), and (16).
   4. evaluate the derivatives using equations (3) - (8).
3. When it is necessary to calculate the initial and final values in Table 13.3
   1. \(T_{in}\), \(P_{in}\), and \(L\) are known constants.
   2. calculate {A,in} and {I,in} using equations (17) and (18).
4. When it is necessary to calculate the quantities of interest, \(T_{out}\), \(P_{out}\), and \(f_A\)
   1. corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), \(\dot{n}_I\), \(T\), and \(P\), spanning the range from their initial (inlet) values to their final (outlet) values will be available.
   2. find \(\dot{n}_{A,out}\) using equation (19).
   3. find or calculate \(T_{out}\), \(P_{out}\), and \(f_A\) using equations (20) -(22).

13.7.3.3 Numerical implementation of the Solution

1. Make the given and known constants available for use in all functions.
2. Write a derivatives function that
   1. receives the independent and dependent variables, \(z\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), \(\dot{n}_I\), \(T\), and \(P\), as arguments,
   2. evaluates the derivatives as described in step 2 of the calculations summary, and returns them..
3. Write a reactor model function that
   1. calculates the initial and final values in Table 13.3 as described in step 3 of the calculations summary,
   2. gets corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), \(\dot{n}_I\), \(T\), and \(P\), spanning the range from their initial values to their final values by calling an IVODE solver and passing the following information to it
      1. the initial values and stopping criterion in Table 13.3 and
      2. the name of the derivatives function from step 2 above, d, checks that the solver successfully solved the IVODEs, and
   3. returns the values returned by the IVODE solver.
4. Perform the analysis by
   1. calling the reactor model function from step 3 above to get corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_Y\), \(\dot{n}_Z\), \(\dot{n}_I\), \(T\), and \(P\), spanning the range from their initial values to their final values, and
   2. calculating the quantities of interest as described in step 4 of the calculations summary.

13.7.3.4 Results and Discussion

The calculateions were performed as described above. The outlet temperature is 363 °C, the outlet pressure is 2.91 atm, and the conversion is 83.3%. This system is similar to that of Example 13.7.1 in that while the feed is at 400 °C and the heat exchange fluid is at 375 °C, the gas leaving the reactor is at 363 °C. Apparently the heat absorbed due to reaction greater than that provided by the heat exchange fluid.

The pressure drop here is only 0.09 atm. It is likely that in this case, ignoring the pressure drop would not have affected the calculated outlet temperature and conversion significantly. However, it is difficult to predict the magnitude of the pressure drop in a packed bed. Consequently, it is wise to account for it in case it proves to be more significant.

SCoRE Connection

Videos showing how to complete this assignment using either Matlab or Python, along with the Matlab and Python code, are available in SCoRE.

13.7.4 Minimum Water-Gas Shift Reactor Volume

The water-gas shift, equation (1), is used to reduce the amount of CO in gas mixtures containing CO, CO₂, H₂, H₂O, and other gases. It is exothermic, \(\Delta H\) = –9120 cal mol^-1, and reversible with the equilibrium constant given by equation (3) with \(K_{0,1}\) = 0.132. The heat capacities of CO, H₂O, CO₂, H₂, and inert, I, can be take to be constant and equal to 29.3, 34.3, 41.3, 29.2, and 40.5 J mol^-1 K^-1, respectively. Two reactors are often used, one operating at higher temperatures and the other at lower temperatures. The steam to CO feed ratio is often in the range from 3 to 6. Suppose the rate in the first reactor when using a certain catalyst is given by equation (2) with \(k_{0.1}\) = 0.0354 mol cm^-3 min^-1 atm^-2 and \(E_1\) = 9740 cal mol^-1. The feed to the adiabatic reactor is at 26 atm and 320 °C, and pressure drop is negligible. Using a feed with 1 mol CO h^-1, 0.359 mol CO₂ h^-1, 4.44 mol H₂ h^-1, and 0.180 mol I h^-1 as a basis, what inlet molar flow of H₂O will minimize the reactor volume if 55% of the CO must be converted? What will the outlet temperature from a reactor of that volume equal?

\[ CO + H_2O \rightleftarrows CO_2 + H_2 \tag{1} \]

\[ r_1 = k_1 \left( P_{CO} P_{H_2O} - \frac{P_{CO_2}P_{H_2}}{K_1} \right) \tag{2} \]

\[ K_1 = K_{0,1} \exp{ \left( \frac{-\Delta H}{RT} \right)} \tag{3} \]

---

Click Here to See What an Expert Might be Thinking at this Point

This assignment describes an adiabatic PFR. The description of the reactor operation does not mention any changes in reactor inputs that might initiate transient behavior, so it is safe to assume that the reactor operates at steady-state. I will summarize the assignment by assigning appropriate variable symbols to all quantities mentioned in the narrative. I’ll use “in” and “out” subscripts to denote values at the reactor inlet or outlet, and I’ll add values of the gas constant since I know I’ll need them.

13.7.4.1 Assignment Summary

Given and Known Constants: \(\Delta H\) = –9120 cal mol^-1, \(K_{0,1}\) = 0.132, \(\hat{C}_{p,CO}\) = 29.3 J mol^-1 K^-1, \(\hat{C}_{p,H_2O}\) = 34.3 J mol^-1 K^-1, \(\hat{C}_{p,CO_2}\) = 41.3 J mol^-1 K^-1, \(\hat{C}_{p,H_2}\) = 29.2 J mol^-1 K^-1, \(\hat{C}_{p,I}\) = 40.5 J mol^-1 K^-1, \(k_{0.1}\) = 0.0354 mol cm^-3 min^-1 atm^-2, \(E_1\) = 9740 cal mol^-1, \(P\) = 26 atm, \(T_{in}\) = 320 °C, \(\dot{n}_{CO,in}\) = 1 mol h^-1, \(\dot{n}_{CO_2,in}\) = 0.359 mol h^-1, \(\dot{n}_{H_2,in}\) = 4.44 mol h^-1, \(\dot{n}_{I,in}\) = 0.180 mol h^-1, \(f_{CO}\) = 0.55, and \(R\) = 1.987 cal mol^-1 K^-1.

Reactor System: adiabatic, steady-state PFR with negligible pressure drop

Quantities of Interest: \(\dot{n}_{H_2O,in,opt} = \underset{\dot{n}_{H_2O,in}}{\arg\min}\left( V \right)\) and \(T_{out}\)

13.7.4.2 Mathematical Formulation of the Solution

Click Here to See What an Expert Might be Thinking at this Point

I’ll need to generate the equations needed to model this reactor and solve them in order to complete this assignment. The reactor is an adiabatic PFR with negligible pressure drop, so I won’t need an energy balance on the heat exchange fluid (because there isn’t one) or a momentum balance (because pressure drop is negligible). So for this assignment the reactor design equations will consist of mole balances and an energy balance on the reacting gas. I’ll write mole balances for each of the five reagents. The general form of the steady-state PFR mole balance is given in Equation 6.39. In this assignment, however, the reactor diameter and length are not mentioned, only the volume. Consequently, both sides of the mole balance can be divided by the cross-sectional area of the reactor. Then noting that \(\frac{\pi D^2}{4}dz\) is equal to a differential volume element, \(dV\), the independent variable can be changed from \(z\) to \(V\). At the same time, the summataion can be written in terms of the one reaction that is taking place.

\[ \frac{d \dot{n}_i}{d z} = \frac{\pi D^2}{4}\sum_j \nu_{i,j}r_j \qquad \Rightarrow \qquad \frac{d \dot{n}_i}{\frac{\pi D^2}{4}dz} = \sum_j \nu_{i,j}r_j \]

\[ \frac{d \dot{n}_i}{dV} = \nu_{i,1}r_1 \]

Having changed the independent variable in the mole balances to \(V\), an analogous change must be made to the general form of the steady-state PFR reacting fluid energy balance, Equation 6.40, after first noting that the reactor is adiabatic so the heat exchange term is equal to zero.

\[ \left(\sum_i \dot{n}_i \hat{C}_{p,i} \right) \frac{d T}{d z} = \cancelto{0}{\pi D U\left( T_{ex} - T \right)} - \frac{\pi D^2}{4}\sum_j r_j \Delta H_j \]

\[ \left(\sum_i \dot{n}_i \hat{C}_{p,i} \right) \frac{d T}{dV} = \sum_j r_j \Delta H_j \]

Expanding the summations and rearranging yields the steady-state energy balance in the form of a derivative expression.

\[ \frac{d T}{dV} = \frac{-r_1 \Delta H_1}{\dot{n}_{CO} \hat{C}_{p,CO} + \dot{n}_{H_2O} \hat{C}_{p,H_2O} + \dot{n}_{CO_2} \hat{C}_{p,CO_2} + \dot{n}_{H_2} \hat{C}_{p,H_2} + \dot{n}_I \hat{C}_{p,I}} \]

Reactor Design Equations

Mole balance design equations for CO, H₂O, CO₂, H₂ and I are presented in equations (4) - (8), and the energy balance on the reacting fluid is given in equation (9).

\[ \frac{d \dot{n}_{CO}}{dV} = - r_1 \tag{4} \]

\[ \frac{d \dot{n}_{H_2O}}{dV} = - r_1 \tag{5} \]

\[ \frac{d \dot{n}_{CO_2}}{dV} = r_1 \tag{6} \]

\[ \frac{d \dot{n}_{H_2}}{dV} = r_1 \tag{7} \]

\[ \frac{d \dot{n}_I}{dV} = 0.0 \tag{8} \]

\[ \frac{d T}{dV} = \frac{-r_1 \Delta H_1}{\dot{n}_{CO} \hat{C}_{p,CO} + \dot{n}_{H_2O} \hat{C}_{p,H_2O} + \dot{n}_{CO_2} \hat{C}_{p,CO_2} + \dot{n}_{H_2} \hat{C}_{p,H_2} + \dot{n}_I \hat{C}_{p,I}} \tag{9} \]

Click Here to See What an Expert Might be Thinking at this Point

The number of IVODE design equations (6) is equal to the number of dependent variables appearing in them (\(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\)), so it is not necessary to eliminate a dependent variable or add an IVODE.

In order to solve the IVODEs numerically, initial values and a stopping criterion are needed. I can define \(V=0\) as the inlet to the reactor so that the remaining intial values become equal to the values of the dependent variables at the reactor inlet. The conversion of CO is specifed, so I will use the correspoinding outlet molar flow of CO as the stopping criterion.

Initial Values and Stopping Criterion

Table 13.4: Initial values and stopping criterion for solving equations, (numbers).

Variable	Initial Value	Stopping Criterion
\(V\)	\(0\)
\(\dot{n}_{CO}\)	\(\dot{n}_{CO,in}\)	\(\dot{n}_{CO,out}\)
\(\dot{n}_{H_2O}\)	\(\dot{n}_{H_2O,in}\)
\(\dot{n}_{CO_2}\)	\(\dot{n}_{CO_2,in}\)
\(\dot{n}_{H_2}\)	\(\dot{n}_{H_2,in}\)
\(\dot{n}_I\)	\(\dot{n}_{I,in}\)
\(T\)	\(T_{in}\)

Click Here to See What an Expert Might be Thinking at this Point

In order to solve the IVODEs numerically I’ll need to do two things: calculate the values of the derivatives at the start of each integration step and calculate all of the initial and final values in Table 13.4.

At the start of each integration step, the independent and dependent variables, \(z\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\), will be known along with the given and known constants. I will need to calculate any other quantities that appear in the derivatives expressions.

The only unknown quantity appearing in equations (4) through (9) is the rate. It can be calculated using equation (2). Before doing so, the rate coefficient, \(k_1\), the equilibrium constant, \(K_1\) and the partial pressures of the reactants and products must be calculated. The rate coefficient can be calculated using the Arrhenius expression, Equation 4.8, and the equilibrium coefficient, using equation (3). No additional unknowns appear in the Arrhenius expression or equation (3). The partial pressures of the reactants can be found by calculating the reactant and product mole fractions and multiplying by the total pressure.

\[ P_i = y_i P = \frac{\dot{n}_i}{\sum_i \dot{n}_i}P = \frac{\dot{n}_i}{\dot{n}_{CO} + \dot{n}_{H_2O} + \dot{n}_{CO_2} + \dot{n}_{H_2} + \dot{n}_{I} + }P \]

Ancillary Equations for Evaluating the Derivatives

\[ k_1 = k_{0,1} \exp{\left( \frac{-E_1}{RT} \right)} \tag{10} \]

\[ P_{CO} = \frac{\dot{n}_{CO}}{\dot{n}_{CO} + \dot{n}_{H_2O} + \dot{n}_{CO_2} + \dot{n}_{H_2} + \dot{n}_I}P \tag{11} \]

\[ P_{H_2O} = \frac{\dot{n}_{H_2O}}{\dot{n}_{CO} + \dot{n}_{H_2O} + \dot{n}_{CO_2} + \dot{n}_{H_2} + \dot{n}_I}P \tag{12} \]

\[ P_{CO_2} = \frac{\dot{n}_{CO_2}}{\dot{n}_{CO} + \dot{n}_{H_2O} + \dot{n}_{CO_2} + \dot{n}_{H_2} + \dot{n}_I}P \tag{13} \]

\[ P_{H_2} = \frac{\dot{n}_{H_2}}{\dot{n}_{CO} + \dot{n}_{H_2O} + \dot{n}_{CO_2} + \dot{n}_{H_2} + \dot{n}_I}P \tag{14} \]

Click Here to See What an Expert Might be Thinking at this Point

When I solve the IVODEs numerically, I’ll also need to calculate the initial and final values in Table 13.4. The inlet molar flow rates of CO, CO₂, H₂, and I, and the inlet temperature are specified in the assignment narrative. I will choose a range of values for the inlet molar flow rate of H₂O and calculate the corresponding reactor volumes to find the minimum volume. Thus, at the time when the IVODEs are being solved, the inlet molar flow rate of H₂O will also be known. The outlet molar flow rate of CO, that is the stopping criterion, can be calculated using the specified CO conversion.

Ancillary Equations for Calculating the Initial and Final Values

\[ \dot{n}_{CO,out} = \dot{n}_{CO,in} \left( 1 - f_{CO} \right) \tag{15} \]

Click Here to See What an Expert Might be Thinking at this Point

At this point I still need a value for inlet the molar flow rate of steam in order to solve the IVODEs. I need to find the value of that flow rate that minimizes the reactor volume. To do that I’ll choose a range of values for the inlet flow rate of steam. The assignment provides some guidance on selecting that range in the statement that the steam to carbon monoxide ratio is normally between 3 and 6.

Having chosen a range of values for the inlet molar flow rate of steam the reactor design equations can be solved numerically for each value in the range to get corresponding sets of values of \(z\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\) spanning the range from their initial (inlet) values to their final (outlet) values. For each inlet steam flow rate, the corresponding reactor volume is the final value of \(V\). By examining the results, I can identify the mimimum volume and the corresponding inlet steam flow rate. I can then re-solve the IVODEs using the optimum steam feed rate to find the outlet temperature.

Ancillary Equations for Calculating the Quantities of Interest

A range of values of the inlet steam molar flow rate spanning the range from three times the inlet CO flow rate to six times it. For each value in the range the reactor design equations can be solved, yielding values of \(z\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\) spanning the range from their initial (inlet) values to their final (outlet) values for that inlet steam flow rate. The reactor volume is simply the final value of \(V\). The minimum volume and the corresponding inlet molar flow rate of steam can then be identified.

\[ \dot{n}_{H_2O,in,opt} = \underset{\dot{n}_{H_2O,in}}{\arg\min}\left( V \right) \\tag{16} \]

The reactor design equations can then be solved using that optimum inlet steam flow rate to verify the minimum volume and to find the outlet temperature.

Calculations Summary

1. Substitute given and known constants into all equations.
2. When it is necessary to evaluate the derivatives
   1. \(z\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\) will be available.
   2. calculate \(K_1\), \(k_1\), \(P_{CO}\), \(P_{H_2O}\), \(P_{CO_2}\), and \(P_{H_2}\) using equations (3) and (10) - (14).
   3. calculate \(r_1\) using equation (2).
   4. evaluate the derivatives using equations (4) - (9).
3. When it is necessary to calculate the initial and final values in Table 13.4
   1. \(\dot{n}_{CO,in}\), \(\dot{n}_{CO_2,in}\), \(\dot{n}_{H_2,in}\), \(\dot{n}_{I,in}\), and \(T_{in}\) are known constants.
   2. a value for \(\dot{n}_{H_2,in}\) will have been chosen.
   3. calculate \(\dot{n}_{CO,out}\) using equation (15).

13.7.4.3 Numerical implementation of the Solution

1. Make the given and known constants available for use in all functions.
2. Define a variable to hold \(\dot{n}_{H_2O,in}\) and make it available to all functions.
3. Write a derivatives function that
   1. receives the independent and dependent variables, \(z\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\), as arguments,
   2. evaluates the derivatives as described in step 2 of the calculations summary, and returns their values.
4. Write a reactor model function that
   1. has access to \(\dot{n}_{H_2O,in}\)
   2. calculates the initial and final values in Table 13.4 as described in step 3 of the calculations summary,
   3. gets corresponding sets of values of \(z\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\), spanning the range from their initial values to their final values by calling an IVODE solver and passing the following information to it
      1. the initial values and stopping criterion in Table 13.4 and
      2. the name of the derivatives function from step 3 above
   4. checks that the solver successfully solved the IVODEs, and
   5. returns the values returned by the IVODE solver.
5. Perform the analysis by
   1. setting a range of values for \(\dot{n}_{H_2O,in}\) and for each value in the range
      1. call the reactor model function from step 4 above to get corresponding sets of values of \(z\), \(\dot{n}_{CO}\), \(\dot{n}_{H_2O}\), \(\dot{n}_{CO_2}\), \(\dot{n}_{H_2}\), \(\dot{n}_{I}\), and \(T\)
      2. save the resulting values of \(V\) and \(T_{out}\)
   2. examining the results to find the value of \(\dot{n}_{H_2O,in}\) where \(V\) was minimized, and
   3. reporting the optimum inlet molar flow rate of steam and the corresponsing reactor volume and outlet temperature.

13.7.4.4 Results and Discussion

The calculations were performed as described above. Figure 13.9 shows the reactor volume as a function of the steam feed rate, and Figure 13.10 shows the outlet temperature. The minimum reactor volume, 2.2 x 10³ cm³, occurs at an H₂O feed rate of 4.82 mol h^-1. The corresponding outlet temperature is 380 °C.

Figure 13.9: Reactor volume as a function of H₂O feed rate.

Figure 13.10: Outlet Temperature as a function of H₂O feed rate.

The results are reasonable, based upon a quantitative analysis. First, as the amount of steam in the feed increases, it is expected that the outlet temperature will decrease if the conversion is held constant. By holding the conversion constant, the heat given off by the reaction is also constant. As the amount of steam in the feed increases, the heat of reaction gets spread across a larger number of moles, and consequently the temperature rise of the gas is smaller. Since the inlet temperature is constant, this means that the average temperature in the reactor decreases as the amount of steam in the feed increases.

With respect to the rate of reaction, increasing the steam in the feed leads to a greater average partial pressure of steam and a lower average temperature in the reactor. Examining the rate expression, it can be seen that decreasing the average temperature will cause the rate coefficient to decrease, and taken alone, this will always cause the rate to decrease. If the rate is decreasing, then the volume should increase. While that eventually does occur, Figure 13.9 shows that at lower steam feed rates, the volume is decreasing, so there must be other factors that are important.

The temperature also affects the equilibrium constant. It will increase as the average temperature decreases (i. e. as the steam feed rate increases). This causes the second term in parentheses in equation (2) to increase. Since that term is being subtracted, increaseing it, taken alone, would also tend to decrease the rate and increase the volume. Thus, the decreasing temperature, taken alone, would lead to a steadily decreasing rate because the rate coefficient would decrease and the term containing the equilibrium constant, which is being subtracted, would increase.

However, increasing the steam feed rate will also lead to a larger average partial pressure of steam in the reactor. The rate expression shows that, taken alone, this would tend to increase the reaction rate. So, the increasing partial pressure of steam tends to increase the rate while the decreasing temperature tends to decrease it. As such, the minimum in the volume seen is Figure 13.9 can be explained qualitatively. At lower steam feed rates, the increased steam partial pressure predominates over the decreased temperature leading to an increase in the rate and a corresponding decrease in the volume needed to reach the fixed conversion. Eventually, the effects of increasing steam partial pressure and decreasing temperature become equal and the volume reaches a minimum. Upon further increase in the steam feed rate, the effect of decreasing temperature predominates over the effect of increasing steam partial pressure, and the rate decreases, leading to an increased reactor volume.

The water-gas shift reaction offers an excellent example of a reversible, exothermic reaction. It was noted in the assignment narrative that two reactors are often used. The reactor considered in this assignment is representative of the first of the two reactors. While the system is far from thermodynamic equilibrium, this reactor can operate at higher temperatures where the rate is larger and the corresponding volume is smaller. However, the reaction approaches equilibrium at conversions that are much smaller than desired.

Therefore in commercial practice, in order to reach higher conversions, the product stream from the first reactor is cooled and fed to a second reactor that operates at much lower temperature. The rate in the second reactor is not as large, due to the lower temperature, but the reaction can proceed to much higher conversion before it approaches equilibrium because the equilibrium constant is much smaller. This situation creates an interesting system design/oprimization situation where the total volume of the two reactors can be minimized with respect to the steam feed rate, the temperature of the feed entering the first reactor, the conversion in the first reactor, and the temperature of the feed entering the second reactor.

SCoRE Connection

Videos showing how to complete this assignment using either Matlab or Python, along with the Matlab and Python code, are available in SCoRE.

13.7.5 Start-up of the PFR from Example 13.7.2

A perfectly insulated PFR with a diameter of 10 cm and a length of 5 m is going to be used for reaction (1). To start up the reactor, a steady, 75 L min^-1 flow of pure water at 25 °C is established. A switching valve is then used to instantaneously change the feed to an aqueous solution containing A and B at concentrations of 1.0 and 1.2 M, respectively. This feed stream is at a constant inlet temperature of 30 °C and flows at the same rate as the water it replaces, 75 L min^-1. Reagents A and B react according to reaction (1) with a rate of reaction that is accurately described by equation (2). The pre-exponential factor in equation (2) is 8.72 x 10⁵ L mol^-1 min^-1 and the activation energy is 7200 cal mol^-1. The heat of reaction (1) is -10,700 cal mol^-1 and may be assumed to be constant. The heat capacity and density of the solution may be taken to be constant and equal to those of water (1.0 cal g^-1 K^-1 and 1.0 g cm^-3). The pressure drop in the reactor is negligible. Plot the molar flow rate of A and the temperature as a function of axial position within the reactor 0.131 minutes after the feed was switched. Plot the same variables again 0.262 min, 0.393 min and 0.524 min after the feed was switched. (Note: the specified times correspond to one-fourth of the space time, one-half of the space time, three fourths of the space time and the space time.)

\[ A + B \rightarrow Y + Z \tag{1} \]

\[ r_1 = k_1C_AC_B \tag{2} \]

---

Click Here to See What an Expert Might be Thinking at this Point

This assignment describes the start-up of a PFR, so the reactor will be operating in a transient mode. However, the changes that are made to initiate the transient only affect the fluid at the reactor inlet. The flow rate of fluid within the reactor does not change, nor does the amount of heat being exchanged through the reactor wall (the reactor is adiabatic). Because there is no mixing in the axial direction, the sudden change in the reagent concentrations and temperature only affect the inlet. The changes will propagate through the reactor as a front, and, in this case, can be described using the steady-state axial profiles before and after the change. I’ll begin by assigning appropriate variable symbols to each quantity mentioned in the assignment. In addition to sub-scripted “in” and “out” to denote quantities at the reactor inlet and outlet, I will use “b” and “a” to indicate values before and after the step changes in concentrations and temperature are applied to the reactor inlet.

13.7.5.1 Assignment Summary

Given and Known Constants: \(D\) = 10 cm, \(L\) = 5 m, \(\dot{V}_{in}\) = 75 L min^-1, \(T_{in,b}\) = 25 °C, \(C_{A,in,b}\) = 0.0 M, \(C_{B,in,b}\) = 0.0 M, \(C_{A,in,a}\) = 1.0 M, \(C_{B,in,a}\) = 1.2 M, \(T_{in,a}\) = 30 °C, \(k_{0.1}\) = 8.72 x 10⁵ L mol^-1 min^-1, \(E_1\) = 7200 cal mol^-1, \(\Delta H_1\) = –10,700 cal mol^-1, \(\tilde{C}_p\) = 1.0 cal g^-1 K^-1, \(\rho\) = 1.0 g cm^-3, \(\tau\) = 0.131, 0.262, 0.393, and 0.524 min, and \(R\) = 1.987 cal mol^-1 K^-1.

Reactor System: Adiabatic PFR with a transient front.

Quantities of Interest: \(\dot{n}_A \left(z\right)\) and \(T\left(z\right)\) as graphs at \(\tau\) = 0.131, 0.262, 0.393, and 0.524 min

13.7.5.2 Mathematical Formulation of the Solution

Click Here to See What an Expert Might be Thinking at this Point

Because the change propagates as a front I can calculate the position of the front as a function of time. The concentration and temperature profiles ahead of the front are the steady-state profiles prior to the switch and those behind the front are the steady-state profiles after the switch. Therefore, I only need to calculate the steady-state profiels prior to the switch and after the switch.

I really don’t need to calculate the front prior to the switch. Pure water at \(T_{in,b}\) is flowing steadily through the reactor. There isn’t any reaction nor a change in temperature, so the profiles are horizontal lines at \(\dot{n}_A\) = 0 and \(T_{in,b}\) for all \(z\).

After the feed switch has been made and the system has reached steady-state, I can use the general forms of the steady-state PFR mole and energy balances to model the system. I don’t need an energy balance on the exchange fluid because there isn’t one, and I don’t need a momentum balance because pressure drop is negligible.

The general form of the mole balance is given by Equation 6.39. There is only one reaction taking place, so the summation reduces to a single term.

\[ \frac{d \dot{n}_i}{d z} = \frac{\pi D^2}{4}\sum_j \nu_{i,j}r_j = \frac{\pi D^2}{4}\nu_{i,1}r_1 \]

The general form of the steady-state PFR reacting fluid energy balance is given by Equation 6.40. The narrative provides the gravimetric heat capacity and the density of the liquid phase reacting fluid, to the first term can be modified to use that information. This PFR is adiabatic, so the heat exchange term is equal to zero, and again, there is only one reaction taking place.

\[ \cancelto{\rho \dot{V} \breve{C}_p}{\left(\sum_i \dot{n}_i \hat{C}_{p,i} \right)} \frac{d T}{d z} = \cancelto{0}{\pi D U\left( T_{ex} - T \right)} - \frac{\pi D^2}{4}\cancelto{r_1 \Delta H_1}{\sum_j r_j \Delta H_j} \]

When I solve the design equations numerically, I’m going to need to evaluate the derivatives, so I will re-write the equation in the form of a derivative expression (see Appendix K).

\[ \frac{d T}{d z} = -\frac{\pi D^2}{4} \frac{r_1 \Delta H_1}{\rho \dot{V} \tilde{C}_p} \]

Reactor Design Equations

Mole balance design equations for A, B, Y, and Z after the feed has been switched and the reactor has reached steady-state are presented in equations (3) through (6). An energy balance on the reacting fluid after the feed has been switched and the reactor has reached steady-state is given in equation (7).

\[ \frac{d \dot{n}_A}{dz} = - \frac{\pi D^2}{4}r_1 \tag{3} \]

\[ \frac{d \dot{n}_B}{dz} = - \frac{\pi D^2}{4}r_1 \tag{4} \]

\[ \frac{d \dot{n}_Y}{dz} = \frac{\pi D^2}{4}r_1 \tag{5} \]

\[ \frac{d \dot{n}_Z}{dz} = \frac{\pi D^2}{4}r_1 \tag{6} \]

\[ \frac{d T}{d z} = -\frac{\pi D^2}{4} \frac{r_1 \Delta H_1}{\rho \dot{V} \tilde{C}_p} \tag{7} \]

Click Here to See What an Expert Might be Thinking at this Point

There are five IVODE reactor design equations and they contain five dependent variables (\(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and %T%), so there isn’t a need to eliminae a dependent variable or add an IVODE.

Initial values and a stopping criterion are needed when solving IVODEs numerically. I can define \(z=0\) to be the inlet to the reactor, in which case the other initial values are the molar flow rates and the temperture at the reactor inlet. The feed only contains A and B, so the inlet molar flow rates of Y and Z are zero. The length of the reactor is given, so that can serve as the stopping criterion.

:::

Initial Values and Stopping Criterion

Table 13.5: Initial values and stopping criterion for solving equations, (numbers).

Variable	Initial Value	Stopping Criterion
\(z\)	\(0\)	\(L\)
\(\dot{n}_A\)	\(\dot{n}_{A,in,a}\)
\(\dot{n}_B\)	\(\dot{n}_{B,in,a}\)
\(\dot{n}_Y\)	\(0\)
\(\dot{n}_Z\)	\(0\)
\(T\)	\(T_{in,a}\)

Click Here to See What an Expert Might be Thinking at this Point

In order to solve the IVODEs numerically I’ll need to do two things: calculate the values of the derivatives at the start of each integration step and calculate all of the initial and final values in Table 13.5. At the start of an integration step, the independent (\(z\)) and dependent variables (\(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\)) will be known, as will the given and known constants listed above. I will need to calculate any other quantities that appear in the derivatives expressions, equations (3) - (7).

In those equations, the reaction rate, \(r_1\), and the volumetric flow rate, \(\dot{V}\), are unknown. The rate can be calculated using the rate expression, equation (2). In order to do that, the rate coefficient and the concentrations of A and B must be calculated. The rate coefficient can be calculated using the Arrhenius expression, Equation 4.8. The concentrations can be calculated using the defining equation for concentration in an open system, Equation 1.15. The reacting fluid is a liquid; assuming it to be an incompressible ideal mixture means that the volumetric flow rate will be constant and equal to the inlet volumetric flow rate.

Ancillary Equations for Evaluating the Derivatives

\[ k_1 = k_{0,1} \exp{\left( \frac{-E_1}{RT} \right)} \tag{8} \]

\[ C_A = \frac{\dot{n}_A}{\dot{V}} \tag{9} \]

\[ C_B = \frac{\dot{n}_B}{\dot{V}} \tag{10} \]

\[ \dot{V} = \dot{V}_{in} \tag{11} \]

Click Here to See What an Expert Might be Thinking at this Point

When I solve the IVODEs numerically, I’ll also need to calculate the initial and final values in Table 13.5. The reactor length, \(L\), and the feed temperature, \(T_{in,a}\) are provided in the assignment narrative, and the inlet molar flow rates of A and B can be calculated from their known inlet concentrations and the inlet volumetric flow rate, Equation 1.15.

Ancillary Equations for Calculating the Initial and Final Values

The inlet molar flow rates can be calculated using equations (12) and (13).

\[ \dot{n}_{A,in} = \dot{V}_{in}C_{A,in} \tag{12} \]

\[ \dot{n}_{B,in} = \dot{V}_{in}C_{B,in} \tag{13} \]

Click Here to See What an Expert Might be Thinking at this Point

At this point the IVODEs can be solved for corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\) that span the range from their initial values to their final values. That is, at this point I will have calculated the profiles of \(\dot{n}_A\) and \(T\) along the length of the reactor at steady-state.

The reacting fluid is an incompressible liquid, so the linear velocity of the front is simply the volumetric flow rate divided by the cross-sectional area of the tubular reactor.

\[ v = \frac{\dot{V}}{\frac{\pi D^2}{4}} = \frac{4 \dot{V}}{\pi D^2} \]

The position of the front at any elapsed time after the switch can be calculated from its velocity.

\[ z_{front} = tv = \frac{4 \dot{V}t}{\pi D^2} \]

As the front propagates through the reactor, the profile ahead of the front will equal the steady-state profile prior to the feed switch and the profile behind the front will equal the steady-state profile after the feed switch.

Solving the reactor design equations yields corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\) that span the range from their initial (feed) values to their final (outlet) values. That is, solving the reactor design equations will yield, among other things, \(\dot{n}_{A,a}\) and \(T_a\) as functions of \(z\) when steady-state has been reached after the feed switch. Prior to the feed switch the molar flow rate of A, \(\dot{n}_{A,b}\), and the temperature, \(T_b\), are constant for all \(z\)

Noting that the fluid is incompressible and the tube diameter is constant, the position of the front at any time following the switch can be calculated using equation (14). The profiles of interest then can be calculated using equations (15) and (16)

\[ z_{front} = \frac{4 \dot{V}t}{\pi D^2} \tag{14} \]

\[ \begin{align} \dot{n}_A\left(z\right) &= \dot{n}_{A,a}\left(z\right) \qquad z \le z_{front} \\ \dot{n}_A\left(z\right) &= \dot{n}_{A,b}\left(z\right) \qquad z > z_{front} \end{align} \tag{15} \]

\[ \begin{align} T\left(z\right) &= T_a\left(z\right) \qquad z \le z_{front} \\ T\left(z\right) &= T_b\left(z\right) \qquad z > z_{front} \end{align} \tag{16} \]

Calculations Summary

1. Substitute given and known constants into all equations.
2. When it is necessary to evaluate the derivatives
   1. \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\) will be available.
   2. calculate \(k_1\) and \(\dot{V}\) using equations (8) and (11).
   3. calculate \(C_A\) and \(C_B\) using equations (9) and (10).
   4. calculate \(r_1\) using equation (2).
   5. evaluate the derivatives using equations (3) through (7)
3. When it is necessary to calculate the initial and final values in Table 13.5
   1. \(T_{in,a}\) and \(L\) are known constants.
   2. calculate \(\dot{n}_{A,in,a}\) and \(\dot{n}_{B,in,a}\) using equations (12) and (13).

13.7.5.3 Numerical implementation of the Solution

1. Make the given and known constants available for use in all functions.
2. Write a derivatives function that
   1. receives the independent and dependent variables, \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\), as arguments,
   2. evaluates the derivatives as described in step 2 of the calculations summary, and returns their values.
3. Write a reactor model function that
   1. calculates the initial and final values in Table 13.5 as described in step 3 of the calculations summary,
   2. gets corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\), spanning the range from their initial values to their final values by calling an IVODE solver and passing the following information to it
      1. the initial values and stopping criterion in Table 13.5 and
      2. the name of the derivatives function from step 2 above, d, checks that the solver successfully solved the IVODEs, and
   3. returns the values returned by the IVODE solver.
4. Perform the analysis by
   1. calling the reactor model function from step 3 above to get corresponding sets of values of \(z\), \(\dot{n}_A\), \(\dot{n}_B\), \(\dot{n}_Y\), \(\dot{n}_Z\), and \(T\), spanning the range from their initial values to their final values for the steady state after the switch
   2. for each of the four elapsed times of interest
      1. calculate the position of the front using equation (14)
      2. plot the molar flow rate of A as a function of \(z\) according to equation (15)
      3. plot the temperature as a function of \(z\) according to equation (16).

13.7.5.4 Results and Discussion

The calculations were performed as described above. Profiles of the molar flow rate of A and the temperature within the reactor 0.131, 0.262, 0.393, and 0.524 min after the feed switch are shown in Figure 13.11. For an incompressible fluid flowing through a PFR at steady-state, the space time is equal to the amount of time the fluid spends within the reactor. Thus, as the figure shows, the front has just reached the outlet of the PFR at a time equal to the space time. For any times greater than this, the profile be invariant with the shape shown in the bottom panel of the figure because after one spece time, the reactor will have reached its new steady state.

Figure 13.11: Concentration (blue) and temperature (red) profiles 0.131, 0.262, 0.393, and 0,524 min after the feed flow started (top to bottom).

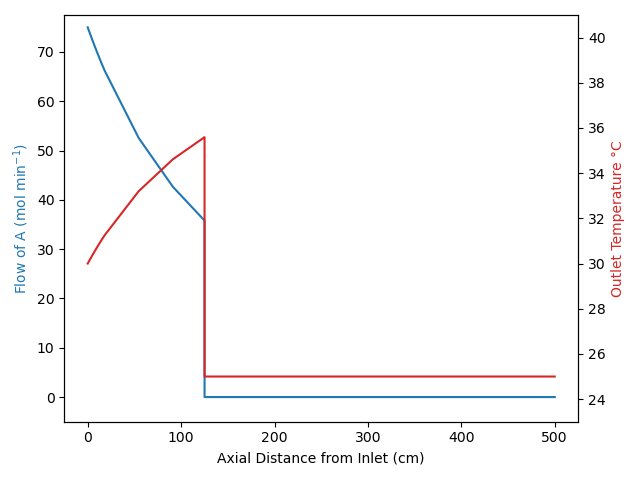
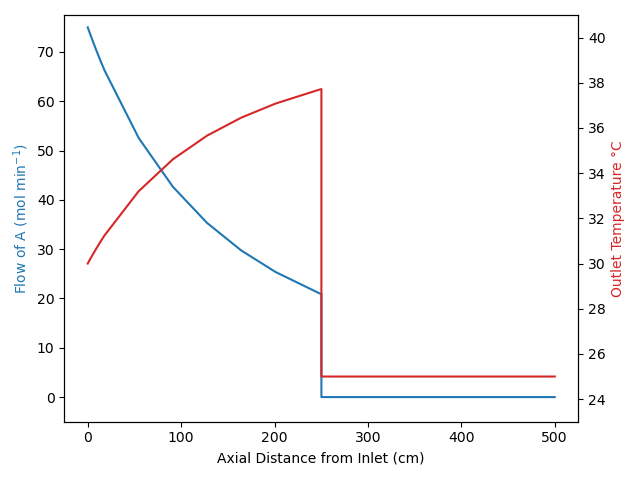
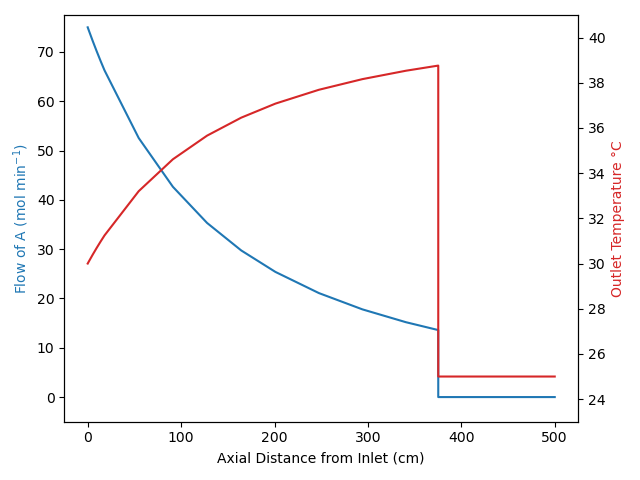
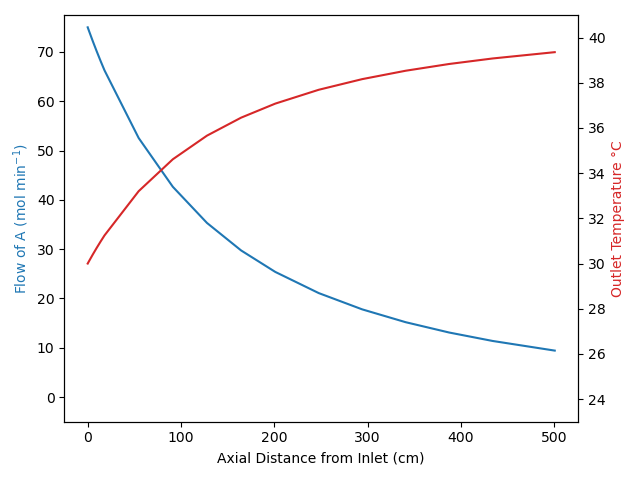
The profiles shown in Figure 13.11 seem a bit unrealistic. Consider what the transient PFR model would predict if only the temperature of the water flowing into this had been changed and without adding reactant to the feed. The model would predict that 0.262 minutes later the temperature of the first half of the reactor would be at 30 °C, and the temperature in the second half of the reactor would be 25 °C, with an abrupt change at the middle of the reactor. A very sharp transition like that is counter-intuitive. Instead, one might expect a smoother transition from hot to cold, not an instantaneous step change. The axial dispersion model presented in Chapter 24 pridicts a smoother, and intuitively more reasonable, temperature transition.

Note

The method of analysis used in this example only applies in the special case where the transient is initiated by step changes in reagent concentration and or temperature at the inlet to the PFR. If the volumetric flow rate had changed, this method of analysis would not be applicable because a change in inlet flow rate affects all of the fluid in the reactor, not just the fluid entering it. Similarly, if there had been heat exchange through the reactor wall and the temperature of the exchange fluid had changed, this method of analysis would not be applicable, again because all of the fluid in the reactor would be affected, not just that entering it.

SCoRE Connection

Videos showing how to complete this assignment using either Matlab or Python, along with the Matlab and Python code, are available in SCoRE.

13.7.6 Gas-Phase Reaction in a Packed-Bed PFR with Internal Concentration Gradients

The gas-phase conversion of A to Z, equation (1), takes place at steady-state in a packed bed PFR operating isothermally at 400 °C. The reaction rate per unit catalyst particle volume is first order in A, equation (2), and at the operating temperature, the rate coefficient is equal to 0.15 cm³_fluid cm³_particle s^-1. The void fraction within the packed bed is equal to 0.4. Pure A, flowing at 1.0 cm³ s^-1 (0.054 g s^-1), 400 °C, and 30 atm is fed to the reactor. There are no temperature gradients anywhere in the reactor or in the catalyst particles, and there are no concentration gradients external to the spherical catalyst particles which have a diameter, \(D_p\) of 4 mm. The effective diffusion coefficient of A within the porous catalyst particles is equal to 0.0029 cm² s^-1 and the gas viscosity may be assumed to be constant and equal to 0.022 cP. If the reactor diameter is 1.5 cm and the conversion of A in the reactor is to equal 85%, what reactor length is required?

\[ A \rightarrow Z \tag{1} \]

\[ r_1 = k_1 C_A \tag{2} \]

---

Click Here to See What an Expert Might be Thinking at this Point

This problem describes operation of an isothermal steady-state PFR. I’ll begin by summarizing the assigmnent, assigning appropriate variable symbols to each quantity it mentions.

13.7.6.1 Assignment Summary

Given and Known Constants: \(T\) = 400 °C, \(k_1\) = 0.15 cm³_fluid cm³_particle s^-1, \(\epsilon\) = 0.4, \(\dot{V}_{in}\) = 1.0 cm³ s^-1, $_{in} = 0.054 g s^-1, \(T_{in}\) = 400 °C, \(P_{in}\) = 30, \(D_p\) = 4 mm, \(D_{A,eff}\) = 0.0029 cm² s^-1, \(\mu\) = 0.022 cP, \(D\) = 1.5 cm, \(f_A\) = 0.85, and \(R\) = 82.06 cm³ atm mol^-1 K^-1.

Reactor System: Isothermal, steady-state PFR

Quantities of Interest: \(L\)

13.7.6.2 Mathematical Formulation of the Solution

Click Here to See What an Expert Might be Thinking at this Point

In order to complete this assignment, I am going to need to generate an appropriate set of reactor design equations and solve them. The reactor design equations must always include mole balances. I will write mole balances for both A and Z. The general form of the steady-state PFR mole balance is shown in Equation 6.39.

\[ \frac{d \dot{n}_i}{d z} =\frac{\pi D^2}{4}\sum_j \nu_{i,j}r_j \]

However, that form of the mole balance assumes that the rate is normalized per volume of reactor (or here per volume of packed bed), that there aren’t any composition or temperature gradients between the fluid and the catalyst particles, and that there aren’t any gradients within the particles. The rate expression provided in the assignment is normalized per catalyst particle volume. Noting that there is only one reaction taking place, the mole balance can be modified to account for the normalization of the rate.

\[ \frac{d \dot{n}_i}{d z} =\frac{\pi D^2}{4}\nu_{i,1}\frac{V_{part}}{V_{bed}}r_1 \]

The particle volume is the bed volume minus the void volume, and the void volume is equal to the bed volume times the void fraction.

\[ \begin{align} \frac{d \dot{n}_i}{d z} &= \frac{\pi D^2}{4}\nu_{i,1}\frac{V_{part}}{V_{bed}}r_1 \\&= \frac{\pi D^2}{4}\nu_{i,1}\frac{V_{bed} - V_{void}}{V_{bed}}r_1 \\&= \frac{\pi D^2}{4}\nu_{i,1}\frac{V_{bed} - \epsilon V_{bed}}{V_{bed}}r_1 = \frac{\pi D^2}{4}\nu_{i,1}\left( 1 - \epsilon \right)r_1 \end{align} \]

That accounts for the rate normalization. The assignment states that there aren’t any gradients external to the particles and that there aren’t any temperature gradients within the particles. However, there may be concentration gradients within the particles. One way to account for any internal concentration gradients is to multiply the rate by the effectiveness factor. Doing so yields a mole balance where the normalization of the rate has been accounted for as have any concentration gradients within the particles.

\[ \frac{d \dot{n}_i}{d z} = \frac{\pi D^2}{4}\nu_{i,1}\left( 1 - \epsilon \right)\eta r_1 \]

The assignment states that the reactor is isothermal and there aren’t any temperature gradients anywhere. In that case, I can solve the mole balance equations independently of the energy balance on the reacting fluid and the energy balance on the heat exchange fluid. Since the assignment does not ask any questions associated with either of those balances, I do not need to include them. The assignment does not mention whether or not there is a pressure drop in the reactor. As such, I’ll need to include a momentum balance in case pressure drop is significant. The steady-state momentum balance for a PFR is given in Equation 6.42.

Reactor Design Equations

Mole balance design equations for A and Z are presented in equations (3) and (4), and a momentum balance is shown in equation (5).

\[ \frac{\dot{n}_A}{dz} = - \frac{\pi D^2}{4}\left(1-\varepsilon \right)\eta r_1 \tag{3} \]

\[ \frac{\dot{n}_Z}{dz} = \frac{\pi D^2}{4}\left(1-\varepsilon \right)\eta r_1 \tag{4} \]

\[ \frac{{dP}}{{dz}} = - \frac{{1 - \varepsilon }}{{{\varepsilon ^3}}}\frac{{{G^2}}}{{\rho {\Phi _s}{D_p}}}\left[ {\frac{{150\left( {1 - \varepsilon } \right)\mu }}{{{\Phi _s}{D_p}G}} + 1.75} \right] \tag{5} \]

Click Here to See What an Expert Might be Thinking at this Point

The reactor design equations consist of three IVODEs and they contain three dependent variables (\(\dot{n}_A\),\(\dot{n}_Z\), and \(P\)) so there isn’t any need to add an IVODE or eliminate a dependent variable.

Initial values and a stopping criterion are needed when solving IVODEs numerically. I can define \(z=0\) as the reactor inlet, in which case the other initial values are simply the values of the dependent variables at the reactor inlet. Here the reactor is fed pure A, so the initial molar flow rate of Z is equal to zero. I know the conversion, so I can calculate the outlet molar flow rate of A and use it as the stopping criterion.

Initial Values and Stopping Criterion

Table 13.6: Initial values and stopping criterion for solving equations, (numbers).

Variable	Initial Value	Stopping Criterion
\(z\)	\(0\)
\(\dot{n}_A\)	\(\dot{n}_{A,in}\)	\(\dot{n}_{A,out}\)
\(\dot{n}_Z\)	\(0\)
\(P\)	\(P_{in}\)

Click Here to See What an Expert Might be Thinking at this Point

In order to solve the IVODEs numerically I’ll need to do two things: calculate the values of the derivatives at the start of each integration step and calculate all of the initial and final values in Table 13.6.

At the start of each integration step \(z\), \(\dot{n}_A\),\(\dot{n}_Z\), and \(P\) will be known along with the given and known constants listed in the assignment summary. I will need to calculate any other quantities that appear in the derivatives expressions. Examination of equations (3) - (5) shows that for this assigment I’ll need to calculate \(\eta\), \(r_1\), \(G\), \(\rho\), and \(\Phi_s\).

The catalyst particles are spherical, so I can calculate the effectiveness factor using Equation 13.32. In order to do that, I will first need to calculate the Thiele modulus for a spherical particle using Equation 13.29 and noting that the particle radius is half of its diameter.

\[ \eta = \frac{3}{\phi}\left( \frac{1}{\tanh{\phi}} - \frac{1}{\phi} \right) \]

\[ \phi = R_{\text{part}}\sqrt{\frac{k}{D_{eA}}} = \frac{D_{\text{part}}}{2}\sqrt{\frac{k}{D_{eA}}} \]

The rate can be calculated using the given rate expression, equation (2), but in order to do so the concentration must first be calculated. Than can be done using the defining equation for concentration in an open system and the ideal gas equation.

\[ C_A = \frac{\dot{n}_A}{\dot{V}} = \frac{\dot{n}_A}{\dot{n}_A + \dot{n}_Z}\frac{P}{RT} \]

The mass flux, \(G\), can be calculated using its definition. To do that, the mass flow rate is needed. Here the inlet mass flow rate is given, but at steady state, the mass flow rate does not change because no nuclear reactions are taking place.

\[ G = \frac{4\dot{m}}{\pi D^2} = \frac{4\dot{m}_{in}}{\pi D^2} \]

I don’t know the molecular weight of A and Z, but I can calculate the density of the fluid by dividing the mass flow rate by the volumetric flow rate, again noting that the mass flow rate is constant and equal to the inlet mass flow rate.

\[ \rho = \frac{\dot{m}}{\dot{V}} = \frac{\dot{m}_{in}P}{\left( \dot{n}_A + \dot{n}_Z \right)RT} \]

Ancillary Equations for Evaluating the Derivatives

\[ \phi = \frac{D_{\text{part}}}{2}\sqrt{\frac{k}{D_{eA}}} \tag{6} \]

\[ \eta = \frac{3}{\phi}\left( \frac{1}{\tanh{\phi}} - \frac{1}{\phi} \right) \tag{7} \]

\[ C_A = \frac{\dot{n}_A}{\dot{n}_A + \dot{n}_Z}\frac{P}{RT} \tag{8} \]

\[ G = \frac{4\dot{m}_{in}}{\pi D^2} \tag{9} \]

\[ \rho = \frac{\dot{m}_{in}P}{\left( \dot{n}_A + \dot{n}_Z \right)RT} \tag{10} \]

Click Here to See What an Expert Might be Thinking at this Point

When I solve the IVODEs numerically, I’ll also need to calculate the initial and final values in Table 13.6. The inlet pressure is given in the assignment narrative. The inlet molar flow rate of A can be calculated using the ideal gas law. Once that has been done, the outlet molar flow rate of A can be calculated using its known conversion.

Ancillary Equations for Calculating the Initial and Final Values

\[ \dot{n}_{A,in} = \frac{\dot{V}_{in}P_{in}}{RT_{in}} \tag{11} \]

\[ \dot{n}_{A,out} = \dot{n}_{A,in} \left( 1 - f_A \right) \tag{12} \]

Click Here to See What an Expert Might be Thinking at this Point

At this point the reactor design equations can be solved numerically to get corresponding sets of values of \(z\), \(\dot{n}_A\),\(\dot{n}_Z\), and \(P\) spanning the range from their initial values to their final values (i.e. from the reactor inlet to the reactor outlet). The final value of \(z\) is the length of the reactor, which is what the assignment asked for.

Solving the reactor design equations yields corresponding sets of values of \(z\), \(\dot{n}_A\),\(\dot{n}_Z\), and \(P\) spanning the range from the reactor inlet to the reactor outlet. The final value of \(z\), then, is the length of the reactor, \(L\).

Calculations Summary

1. Substitute given and known constants into all equations.
2. When it is necessary to evaluate the derivatives
   1. \(z\), \(\dot{n}_A\),\(\dot{n}_Z\), and \(P\) will be available.
   2. calculate \(\phi\), \(C_A\), \(G\), and \(\rho\) using equations (6), (8), (9), and (10).
   3. calculate \(\eta\) using equation (7).
   4. evaluate the derivatives using equations (3) - (5).
3. When it is necessary to calculate the initial and final values in Table 13.6
   1. \(P_{in}\) is a known constant.
   2. calculate \(\dot{n}_{A,in}\) and \(\dot{n}_{A,out}\) using equations (11) and (12)

13.7.6.3 Numerical implementation of the Solution

1. Make the given and known constants available for use in all functions.
2. Write a derivatives function that
   1. receives the independent and dependent variables, \(z\), \(\dot{n}_A\),\(\dot{n}_Z\), and \(P\), as arguments,
   2. evaluates the derivatives as described in step 2 of the calculations summary, and returns their values.
3. Write a reactor model function that
   1. alculates the initial and final values in Table 13.6 as described in step 3 of the calculations summary,
   2. gets corresponding sets of values of \(z\), \(\dot{n}_A\),\(\dot{n}_Z\), and \(P\), spanning the range from their initial values to their final values by calling an IVODE solver and passing the following information to it
      1. the initial values and stopping criterion in Table 13.6 and
      2. the name of the derivatives function from step 3 above, d, checks that the solver successfully solved the IVODEs, and
   3. returns the values returned by the IVODE solver.
4. Perform the analysis by
   1. calling the reactor model function from step 3 above to get corresponding sets of values of \(z\), \(\dot{n}_A\),\(\dot{n}_Z\), and \(P\), spanning the range from their initial values to their final values.
   2. extracting the final value of \(z\), which is the length of the reactor \(L\).

13.7.6.4 Results and Discussion

The calculations were performed as described above. During the calculations it is found that the effectiveness factor is 0.885, resulting in a reactor length of 13.5 cm. If the effectiveness factor was not used to correct for the concentration gradients within the catalyst particles, a significantly shorter length of 11.9 cm would have been calculated corresponding to an error of almost 12%.

The calculations also show that the pressure drop is negligible; the calculated outlet pressure is 30 atm, which is equal to the inlet pressure. Nonetheless, this calculation was necessary because there was no way of knowing ahead of time whether the pressure drop would be significant.

Note

This example serves to show that when a reacting system consists of more than one phase, it is essential to check for gradients in the fluid phases close to interfaces and, if there are porous solids, within the pores. The equations developed and used in Reaction Engineering Basics assume that the reacting fluid is homogeneous, i. e. that no such gradients exist. Using those reactor design equations to model systems where gradients do exist can result is significant error.

There are much more rigorous ways to account for gradients in a reacting system. Doing so is often a substantial component of intermediate and advanced reaction engineering textbooks and courses.

SCoRE Connection

Videos showing how to complete this assignment using either Matlab or Python, along with the Matlab and Python code, are available in SCoRE.

13.8 Symbols Used in Chapter 13

Symbol	Meaning
\(ex\)	Subscript denoting the heat exchange fluid.
\(f\)	Friction factor.
\(i\)	Subscript denoting a fluid phase reagent.
\(j\)	Subscript denoting a reaction occurring in the system.
\(j_D\)	Dimensionless \(j\) factor for mass transfer.
\(k_c\)	Concentration based mass transfer coefficient.
\(\dot{m}_{ex}\)	Mass flow rate of the exchange fluid.
\(\dot{n}_i\)	Molar flow rate of reagent \(i\); an additional subscripted “in” denotes the inlet value; an additional subscripted “out” denotes the outlet value.
\(r_j\)	Net rate of reaction \(j\) per unit volume of reacting fluid.
\(t\)	Time.
\(z\)	Distance from the inlet along the axis of a PFR.
\(A\)	Heat transfer area.
\(C_i\)	Concentration of reagent \(i\); an additional subscripted “out” denotes the outlet value, “in” denotes the inlet value, or “0” denotes the initial value.
\(\tilde C_{p,ex}\)	Mass-specific heat capacity of the exchange fluid.
\(\tilde C_{p}\)	Mass-specific heat capacity of the reacting fluid.
\(\breve C_{p,ex}\)	Volume-specific heat capacity of the exchange fluid.
\(\breve C_{p}\)	Volume-specific heat capacity of the reacting fluid.
\(\hat C_{p,ex}\)	Molar heat capacity of the exchange fluid.
\(\hat C_{p,i}\)	Molar heat capacity of reagent \(i\).
\(D\)	Diameter of a PFR.
\(D_A\)	Diffusion coefficient for reagent A; an additional subscripted “eff” denotes an effective diffusion coefficient.
\(L\)	Length of a PFR.
\(M_{ex}\)	Molecular weight of the exchange fluid.
\(N_{Re}\)	Reynold’s number.
\(P\)	Pressure of the reacting fluid.
\(P_i\)	Partial pressure of reagent \(i\).
\(\dot Q\)	Rate of heat transfer from the exchange fluid to the reacting fluid.
\(R\)	Ideal gas constant.
\(T\)	Temperture of the reacting fluid; an additional subscripted “in” denotes the inlet value; an additional subscripted “0” denotes the initial value.
\(T_{ex}\)	Temperature of the exchange fluid within the shell/jacket and at the outlet; an additional subscripted “in” denoes the inlet value.
\(U\)	Heat transfer coefficient.
\(V\)	Volume of reacting fluid within a reactor.
\(\dot{V}\)	Volumetric flow rate of the reacting fluid; an additional subscripted “in” denotes the value at the inlet.
\(V_{ex}\)	Volume of exchange fluid contained within the reactor shell/jacket.
\(\dot{W}\)	Rate at which the reacting fluid does work on the surroundings via shafts, moving boundaries, etc.
\(\gamma\)	Fraction of the exchange fluid that undergoes phase change or term defined in Equation 13.35.
\(\delta\)	Boundary layer thickness.
\(\epsilon\)	Bed void fraction.
\(\varepsilon\)	Catalyst particle void fraction.
\(\eta\)	Effectiveness factor; a subscripted “G” denotes the global effectiveness factor.
\(\mu\)	Viscosity.
\(\nu_{i,j}\)	Stoichiometric coefficient of reagent \(i\) in reaction \(j\).
\(\rho\)	Density of the reacting fluid.
\(\rho_{ex}\)	Density of the exchange fluid.
\(\tau\)	Pore tortuosity.
\(\tau_{PFR}\)	PFR space time.
\(\phi\)	Thiele modulus.
\(\Delta H_j\)	Heat of reaction \(j\).
\(\Delta H_{\text{latent},ex}^0\)	Latent heat for the phase change the exchange fluid undergoes.