Appendix F — Mathematics
Reaction Engineering Basics assumes that reactor model equations will be solved numerically. This appendix presents an overview of the types of equations that are encountered, the quantities that appear in them, and their numerical solution. It also considers estimation of parameters using numerical methods.
F.1 Quantities Appearing in Equations
Equations establish a relationship among different quantities. When solving equations numerically, the quantities appearing in them can be grouped based upon the way they are used or processed. For the purposes of this appendix, each quantity appearing in an equation can be assigned to one of the following categories.
- Known Constants
- Quantities whose values are known and do not change throughout the analysis.
- Variables
- Quantities whose values are not known, but are found by solving the equations. In differential equations variables are further categorized as the independent variable or a dependent variable.
- Derivatives
- Quantities representing the change of a dependent variable relative to a change in the independent variable.
- Additional Unknowns
- Quantities that are not variables and whose values are not known.
- Parameters
- Quantities whose values are constant any one time the equations are solved, but that have different values each time they are solved. Parameters can be further categorized as being either specified or to be estimated.
F.2 ATEs
Algebraic-transcendental equations (ATEs) are one of the equation types that must be solved when performing reaction engineering tasks. (The acronym ATE is used in this book, but it is not generally used in other books or online.) In the context of Reaction Engineering Basics, ATEs are easily identifiable because they are the only equation type that does not contain derivatives. Slightly more specifically, a set of ATEs is a group of 1 or more mathematical equations that may involve or contain math operations (addition, subtraction, multiplication, and division). Terms in ATEs can be exponents or bases that are raised to some power, and they can appear in transcendental functions. Exponential functions are the most common transcendental functions appearing in the ATEs found in Reaction Engineering Basics. They arise any time an equation includes a rate coefficient that displays Arrhenius temperature dependence, Equation 4.8.
F.3 ODEs
Some of the ideal reactor design equations are partial differential equations, but in Reaction Engineering Basics, they are always simplified to linear, first-order, ordinary differential equations (ODEs) before they need to be solved. As a reminder, in linear, first-order, ordinary differential equations, only ordinary first derivatives appear, they are not multiplied or divided by other derivatives, and they are not raised to any power other than one.
In sets of ODEs that are solved in Reaction Engineering Basics, the independent variable is the same in every derivative in the set. A set of \(N\) ODEs must contain the derivatives of \(N\) dependent variables with respect to the independent variable. The set of ODEs applies within a continuous interval of the independent variable. Each of the dependent variables then span their own corresponding range of values.
Most generally, a set of ODEs will take the form shown in Equations F.1 through F.4. In those equations \(z\) is the independent variable; \(y_1\), \(y_2\), \(y_3\), and \(y_4\) are the dependent variables; and \(m_{1,1}\) through \(m_{4,4}\) and \(g_1\) through \(g_4\) can be constants (including zero) or functions of the independent and dependent variables. While four equations are being used here for illustration purposes, there can be any number of ordinary differential equations in the set as long as the number of ordinary differential equations is equal to the number of dependent variables, and there is only one independent variable.
\[ m_{1,1}\frac{dy_1}{dz} + m_{1,2}\frac{dy_2}{dz} + m_{1,3}\frac{dy_3}{dz} + m_{1,4}\frac{dy_4}{dz} = g_1 \tag{F.1}\]
\[ m_{2,1}\frac{dy_1}{dz} + m_{2,2}\frac{dy_2}{dz} + m_{2,3}\frac{dy_3}{dz} + m_{2,4}\frac{dy_4}{dz} = g_2 \tag{F.2}\]
\[ m_{3,1}\frac{dy_1}{dz} + m_{3,2}\frac{dy_2}{dz} + m_{3,3}\frac{dy_3}{dz} + m_{3,4}\frac{dy_4}{dz} = g_3 \tag{F.3}\]
\[ m_{4,1}\frac{dy_1}{dz} + m_{4,2}\frac{dy_2}{dz} + m_{4,3}\frac{dy_3}{dz} + m_{4,4}\frac{dy_4}{dz} = g_4 \tag{F.4}\]
In reactor design equations the dependent variables (\(y_i\)’s above) will be things such as molar amounts or molar flow rates, temperature, pressure, and volumes or volumetric flow rates. The independent variable is either the distance from the reactor inlet (\(z\)) or time (\(t\)).
F.3.1 IVODEs
The second equation type that must be solved when performing reaction engineering tasks is called an initial-value ODE (IVODE). ODEs apply over a continuous interval of the independent variable, \(z\), beginning at its initial value and increasing or decreasing monotonically to its final value. Very often the initial value can be defined to be \(z=0\), and \(z\) increases to its final value. At any value of the independent variable, each dependent variable has a corresponding value. The values of the dependent variables corresponding to the initial value of \(z\) are called thier initial values, and those corresponding to the final value of \(z\) are their final values. The distinguishing characteristics of IVODEs are that (a) all of the initial values are known or can be calculated directly and (b) only one final value (either for the independent variable or for one of the dependent variables) is known or can be calculated directly.
F.3.2 DAEs
Differential-algebraic equations (DAEs) are the final type of equation that must be solved when completing tasks in Reaction Engineering Basics. In a set of DAEs, a set of IVODEs is coupled to set of ATEs. The distinguishing feature of a set of DAEs is that neither the set of IVODEs nor the set of ATEs can be solved independently of the other set.
There are two situations where DAEs are encountered in Reaction Engineering Basics. In the first situation, either a constant appearing in the IVODEs or the initial value of one of the dependent variables is an additional unknown. At the same time, two final values are known, and the additional unknown is implicitly related to one of the known final values. The second situation is encountered when analyzing thermally backmixed and recycle PFRs. In this situation, both the initial and final values for one or more dependent variables are unknown, but they are explicitly related through ATEs.
F.3.3 BVODEs
The design equations for the axial dispersion reactor model are boundary-value ODEs (BVODEs). BVODEs are the third type of equation that must be solved when completing reaction engineering tasks. Criteria for identifying them are not needed because the only time they are encountered in Reaction Engineering Basics is when modeling a reactor with axial dispersion. The limits of the continuous interval of the independent variable for a set of BVODEs are referred to as its upper and lower bounds, and not as initial and final values.
F.4 Important Equation Formats
When solving equations numerically, they often must be formatted appropriately. ATEs must be rewritten as a corresponding set of residuals expressions, and IVODES must be converted to a set of derivative expressions. These equation formats are considered in this section.
F.4.1 Residual Expressions
In preparation for numerically solving a set of ATEs, each equation must be rewritten as a residual expression. Doing so is trivially simple. If there is a zero on either side of the equals sign, no rearrangement is necessary. If not, everything on one side of the equals sign should be subtracted from both sides of the equation. This will result in an equation with a zero on one side of the equals sign. The nonzero side of that equation is called a residual. A residual expression is created by choosing a variable to represent the residual and setting it equal to the nonzero side of the equation. In Reaction Engineering Basics, \(\epsilon\) is usually used to represent residuals.
As an example, consider the typical ATE mole balance shown in Equation F.5. It does not have a zero on either side of the equals sign, so the right side of the equation, \(\dot{n}_{A,1} + rV\), is subtracted from both sides, leading to Equation F.6. Letting \(\epsilon\) represent the residual, the corresponding residual expression, Equation F.7, is written by setting \(\epsilon\) equal to the non-zero side of Equation F.6
\[ \dot{V}C_{A,0} = \dot{n}_{A,1} + rV \tag{F.5}\]
\[ \dot{V}C_{A,0} - \dot{n}_{A,1} - rV =0 \tag{F.6}\]
\[ \epsilon = \dot{V}C_{A,0} - \dot{n}_{A,1} - rV \tag{F.7}\]
If a set of \(N\) ATEs is being solved, they must be converted into a set of \(N\) residual expressions. In general each residual can be a function of all of the ATE variables. Substitution of a solution (i.e. a set of ATE variables that solve the ATEs) will cause all of the residuals to evaluate to zero.
F.4.2 Derivative Expressions
In preparation for solving a set of \(N\) IVODEs, they should be rearranged into a set of derivative functions if they aren’t already in that form. For example, Equations F.1 through F.4 need to be converted to derivative expressions of the form shown in Equations F.8 through F.11 where \(f_1\), \(f_2\), \(f_3\), and \(f_4\) each may be a function of \(z\), \(y_1\), \(y_2\), \(y_3\), and \(y_4\).
\[ \frac{dy_1}{dz} = f_1 \tag{F.8}\]
\[ \frac{dy_2}{dz} = f_2 \tag{F.9}\]
\[ \frac{dy_3}{dz} = f_3 \tag{F.10}\]
\[ \frac{dy_4}{dz} = f_4 \tag{F.11}\]
That can be accomplished by algebraic manipulation of Equations F.1 through F.4, but it is particularly straightforward if the original IVODEs are written as a matrix equation. The coefficients in Equations F.1 through F.4, \(m_{1,1}\), \(m_{1,2}\), etc., can be used to construct a so-called mass matrix, \(\boldsymbol{M}\), as shown in Equation F.12, the dependent variables can be used to construct a column vector, \(\underline{y}\), as in equation Equation F.13, and the functions, \(g_1\), \(g_2\), \(g_3\), and \(g_4\), can be used to construct a column vector, \(\underline{g}\), as in equation Equation F.14.
\[ \boldsymbol{M} = \begin{bmatrix} m_{1,1} \ m_{1,2} \ m_{1,3} \ m_{1,4} \\m_{2,1} \ m_{2,2} \ m_{2,3} \ m_{2,4} \\m_{3,1} \ m_{3,2} \ m_{3,3} \ m_{3,4} \\ m_{4,1} \ m_{4,2} \ m_{4,3} \ m_{4,4} \end{bmatrix} \tag{F.12}\]
\[ \underline{y} = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \end{bmatrix} \tag{F.13}\]
\[ \underline{g} = \begin{bmatrix} g_1 \\ g_2 \\ g_3 \\ g_4 \end{bmatrix} \tag{F.14}\]
Equations F.1 through F.4 then can be written as a matrix equation, Equation F.15. Pre-multiplying each side of Equation F.15 by the inverse of the mass matrix yields the desired derivative expressions, Equation F.16. That is, comparing Equation F.16 to Equations F.8 through F.11, it is apparent that they are equivalent with \(f_1\), \(f_2\), \(f_3\), and \(f_4\) given by Equation F.17.
\[ \boldsymbol{M}\frac{d}{dz}\underline{y} = \underline{g} \tag{F.15}\]
\[ \frac{d}{dz}\underline{y} = \boldsymbol{M}^{-1} \underline{g} \tag{F.16}\]
\[ \begin{bmatrix} f_1 \\ f_2 \\ f_3 \\ f_4 \end{bmatrix} = \underline{f} = \boldsymbol{M}^{-1} \underline{g} \tag{F.17}\]
F.5 Solving Equations
Equations are solved numerically by calling a function, known as a solver, from a mathematics software package. The documentation for the solver will specifiy the details including the arguments that must be provided and the results that will be returned. It will also stipulate the format and order in which the arguments must be passed and results will be returned.
The equations to be solved must be provided to the solver, and most commonly they are provided in the form of a function. The engineer solving the equations must write this function, but the solver documentation will specify its arguments, their format and their order and the values it must return, their format and their order. The engineer cannot add or remove arguments or return values because the solver will call this function assuming it meets the solver’s specifications. An important consequence of this is that if the function providing the equations requires input other than the specified arguments, that input must be made available by some other means.
There are numerous mathematics software packages that provide solvers. For any one type of solver (ATE, IVODE, BVODE) the specifications may vary from one mathematics software package to the next, but the required input is essentially the same irrespective of the software package. The information provided in Reaction Engineering Basics is sufficient for understanding the examples that are presented, and it is presented in a manner that allows the reader to solve equations using whatever mathematics software they choose.
Readers who seek further details are encouraged to consult the documentation for the software package they are using or to consult references on numerical methods.
F.5.1 Solving ATEs
A set of \(N\) ATEs can be solved to find the values of the \(N\) variables appearing in the ATEs. A set of ATEs can have more than one solution. An ATE solver is a computer function that solves a set of ATEs numerically. This sub-appendix describes the input required by ATE solvers, how they work, the results they return, and potential issues that can arise when using them.
F.5.1.1 ATE Solver Input
Typically, an ATE solver must be provided with two inputs. The first is an initial guess for the solution, and the second is a residuals function. Depending upon the mathematics software being used, the solver may accept other input. The order and formatting of the arguments also vary between mathematics software packages.
F.5.1.1.1 The Initial Guess for the ATE Variables
As just noted, when an ATE solver is first called, it must be provided with an initial guess for a solution. Providing an acceptable guess is not usually difficult. In reaction engineering analyses, the ATE variables have a physical meaning. That, together with a qualitative understanding of reactor performance, provides guidance for making an initial guess. An initial guess that involves small changes in reacting fluid temperature and reagent flow rates will generally result in convergence to a solution.
In this book, examples that involve solution of sets of ATEs will have “Click Here to See What an Expert Might be Thinking at this Point” callouts that discuss the choice of the initial guess for that set of equations. If the original guess does not lead to convergence, that will be also be noted, and an explanation will be provided that describes the reasoning used to improve the initial guess so that conversion was achieved.
Similarly, some of the ATEs that are solved in Reaction Engineering Basics have multiple solutions. When that is the case, the example will describe how the initial guesses leading to each solution were generated. Also, Example 12.7.4 shows a method for determining whether a set of ATEs has multiple solutions and finding those solutions.
F.5.1.1.2 The Residuals Function
The other required input to an ATE solver is a residuals function. The purpose of the residuals function is to evaluate the residuals, given a guess for the solution. The engineer solving the ATEs must write the residuals function, but because it will be called by the ATE solver, the arguments passed to it and the values it returns are specified by the ATE solver. The arguments to the residuals function are guesses for the ATE variables, and it always returns the corresponding values of the ATE residuals.
If additional input variables are needed for calculating the residuals, that input must be made available to the residuals function by some means other than passing them as arguments. The documentation for the solver may suggest a preferred way to do this, such as by using a global variable or by using a pass-through function.
F.5.1.2 How ATE Solvers Work
Effectively, the ATE solver uses an iterative, trial and error process to find a solution.
- The ATE residuals corresponding to the initial guess are calculated and retained as the best solution so far.
- The ATE solver generates a new guess and calculates the corresponding ATE residuals.
- The residuals corresponding to the new guess and the best solution so far are compared.
- Whichever guess gave residuals that are closer to zero is retained as the best solution so far
- Steps 2 through 4 are repeated until the solver determines that either
- the best solution so far is acceptably close to the exact solution, or
- it cannot find a solution that is acceptably close to the exact solution.
For details on how the solver generates guesses, how it determines which set of residuals is closer to zero, and the criteria for the determinations in step 5, one can consult the documentation for the solver being used and reference works on numerical methods.
F.5.1.3 Convergence and Solver Issues
Ideally, the ATE residuals should get closer and closer to zero with each iteration. This is called convergence to a solution. The solution returned by the solver will not be exact, but it will be “very close” to the exact solution. Put differently, when a converged solution is found, the difference between the solution returned by the solver and the exact solution is negligible. If the solver is unable to converge to the point where the residuals are “very close” to zero, it will print an error message and/or return a flag variable indicating that it did not converge and why.
ATE solvers can fail to converge for different reasons, and for each reason, there are corrective actions that can be taken. Nonetheless, if the initial guess provided to the solver is “close enough” to a solution, the solver will converge. When the ATE solver fails to converge it is a good idea to check the inaccurate solution it returned. If an ATE variable in that solution is absurdly large or small, it often indicates that these is an error in the computer code or that the units being used in the calculations are not consistent. Otherwise, the inaccurage solution, together with a qualitative understanding of reactor performance, may suggest a way to revise the initial guess so that the solver does converge.
Finally, as already noted, sets of ATEs can have more than one solution. If a set of ATEs has multiple solutions, most ATE solvers will only find one of them. To find other solutions, the solver should be called again using a different initial guess.
F.5.1.4 ATE Solver Return Values
Even if it fails to converge, an ATE solver will return two things. The first is the best solution it was able to find and the second is some indicator of whether it converged. The latter might be a boolean variable or an integer where the value of the integer indicates convergence or the reason why the solver stopped iterating. Some solvers also return a text string that provides a brief explanation of the reason why it stopped trying to improve the solution.
F.5.1.5 Formulating the Calculations for Solving ATEs
Chapter 8.4 outlines a workflow for completing reaction engineering tasks or assignments that includes formulating the calculations for solving equations numerically. When solving ATEs, the formulation of the calculations will include specifications for the residuals function and specifications for a reactor function.
The specifications for the residuals function should list the ATE variables as its arguments and the corresponding ATE residuals as its return variables. If any other variables need to be made available to the residuals function, its specifications should list them. Finally, the residuals function specifications should include an algorithm that lists a sequence of equations that can be used to calculate the ATE residuals starting from known constants, the ATE variables and the variables that have been made available to the residuals function.
The specifications for the reactor function may list arguments or it may indicate that it doesn’t take any arguments. More importantly, the specifications will list the ATE variables as the return values. The algorithm will define an initial guess for the ATE variables, make variables listed in the residuals function available to it, call the ATE solver, and return the solution found by the solver. Before returning the solution, it should verify that the solver did, in fact, converge, but typically the algorithm won’t list this in the sequence of equations.
F.5.2 Solving IVODEs
A set of IVODEs applies in an interval of the independent variable, beginning at its initial value and ending at its final value. There will be \(N\) dependent variables and one independent variable in a set of \(N\) IVODEs. The numerical solution of a set of IVODEs consists of sets of values (i. e. vectors) of the independent variable and each dependent variable. The sets all contain the same number of values. The values of the independent variable begin at its initial value and increase or decrease monotonically to its final value. For each dependent variable, the nth value is the value of that dependent variable corresponding to the nth value of the independent variable. A brief way of describing the numerical solution of a set of IVODEs is as sets of corresponding values of the independent and dependent variables spanning the range from their initial to their final values. An IVODE solver is a computer function that solves a set of IVODEs numerically. This sub-appendix describes the input required by IVODE solvers, how they work, the results they return, and potential issues that can arise when using them.
F.5.2.1 IVODE Solver Input
Typically an IVODE solver must be provided with three inputs. The first is the initial values of the independent and dependent variables. The second is a stopping criterion, and the third is a derivatives function. Depending on the mathematics software package being used, the solver may accept other input. The order and formatting of the arguments and return values will vary from one software packge to another.
F.5.2.1.1 Initial Values and Stopping Criterion
The engineer solving the IVODEs can usually define the initial value of the independent variable. Most commonly it is difined to equal zero. The value of each dependent variable when the independent variables is at its initial value are their initial values. With IVODEs, all of the initial values will be known or it will be possible to calculate them directly. Either the final value of the independent variable or the final value of one of the dependent variables will also be known, or it will be possible to calculate it directly. The identity of the variable for which the final value is known, along with that final value, make up the stopping criterion that must be provided as the second argument to the IVODE solver.
F.5.2.1.2 The Derivatives Function
The final argument that must be provided to the IVODE solver is the derivatives function. The purpose of the derivatives function is to evaluate the derivative of each dependent variable with respect to the independent variable, given values for the independent and dependent variables. It is written by the engineer who needs to solve the IVODEs, but is called by the IVODE solver. For that reason, the solver specifies the arguments and return values. Typically, the only arguments to the derivatives function are the independent and dependent variables and the only return values are the corresponding values of the derivatives. The solver sets how those quantities are formatted and the order in which they are passed or returned. If additional input variables are needed for evaluating the derivatives, that input must be made available to the derivatives function by some other means than passing them as arguments.
F.5.2.2 How IVODE Solvers Work
An IVODE solver starts from the initial values, as illustrated graphically in panel (a) of Figure F.1 for any one of the dependent variables, \(y_i\). It isn’t possible to plot \(y_i\) vs. \(z\) at that point because \(y_i\left(z\right)\) is not known. (Indeed, \(y_i\left(z\right)\) is the solution to the IVODE.) Instead, the solver uses the derivatives function to calculate the value of each of the derivatives at \(\left(z_0,y_{i,0}\right)\). The derivative, \(\frac{dy_i}{dz}\), at that point is the unknown slope of the function at \(\left(z_0,y_{i,0}\right)\). This is shown graphically in panel (b) of Figure F.1.
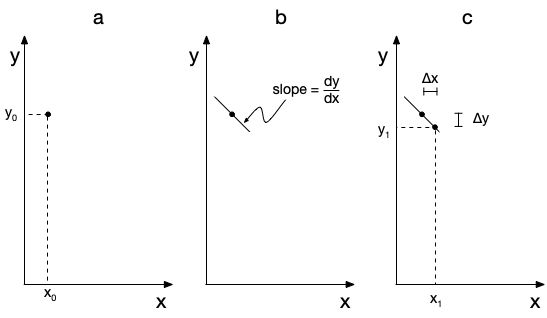
The solver then approximates \(y_i\) vs. \(z\) as a straight line with that slope. It only does that over a small increment in the independent variable known as the integration step size and indicated in the figure as \(\Delta z\). The resulting point, \(\left(z_1,y_{i,1}\right)\), is shown in panel (c) of Figure F.1. This process is sometimes referred to as taking an integration step. Effectively, the solver uses the small straight line segment between \(\left(z_0,y_{i,0}\right)\) and \(\left(z_1,y_{i,1}\right)\) to approximate the true solution, \(y_i\left(z\right)\), in that interval. The accuracy of this approximation increases as \(\Delta z\) decreases, so typically the solver uses small steps. A new integration step is then taken starting from \(\left(z_1,y_{i,1}\right)\).
Of course, the solver eventually must stop taking integration steps. After completing each step, the solver checks to determine whether making that step resulted in the stopping criterion being satisfied. If not, the solver takes another integration step. If the stopping criterion has been exceeded, the step size is adjusted to that the stopping criterion is satisfied exactly. The solver then returns the values of the dependent variables and the independent variable for all of the steps it took while solving the IVODEs, including those final interpolated values.
That was a simplified summary of how an IVODE solver works. For details on how the solver chooses the step size and other variations on how it works, one can consult the documentation for the solver being used and reference works on numerical methods.
F.5.2.3 IVODE Solver Issues
Generally IVODE solvers are quite robust when solving the kinds of ODEs encountered in introductory reaction engineering courses. However, there are three issues to be aware of. The first is failure to reach the known final value of a dependent variable. When the final value of a dependent variable is being used as the stopping criterion, many solvers require the user to provide both that final value and a final value for the independent variable. The solver then takes steps as described above, and after each step it checks to see whether either variable has reached its specified final value. If the final value of the independent variable is too small, the solver may reach that value first and stop. As a consequence, the known final value of the dependent variable will not have been reached, and the result that is returned will not span the full interval wherein IVODEs apply. Therefore it is important to check the solution and verify that the dependent variable reached its known final value.
To avoid having the solver stop because it reached the stopping criterion for the independent variable, it is tempting to specify a very large final value for it. This could result in the second solver issue. The initial step size used by the solver often increases when the final value of the independent variable is increased. In some extreme cases, if the initial step size becomes too large, the linear approximation indicated in Figure F.1 is not valid, resulting in an inaccurate solution. Therefore, it is important to check that the step size was not too large. The solution that is returned will include the final value of the independent variable. If it is orders of magnitude smaller than the guess provided to the solver, the solution can be repeated using a final value for the independent variable that is only slightly greater than the value returned the first time the IVODEs were solved.
The third possible issue arises when solving sets of IVODEs where one of the dependent variables changes very abruptly over a very small range of the independent variable. The abrupt changes in that dependent variable may significantly affect the other dependent variables over a much broader range of the independent variable. Equations like this are called stiff ODEs, and they require special treatment of the step size. Therefore, when solving sets of ODEs, one should pay attention to whether any of the dependent variables change very abruptly as the independent variable changes. If they do, it is advisable to repeat the solution using a solver that is specifically tailored to stiff ODEs.
F.5.2.4 IVODE Solver Return Values
As noted above, the solution of a set of IVODEs is a set of corresponding values of the independent and dependent variables spanning the range from their initial to their final values. The first value in each set will be the initial value of that variable. The rest of the values in the set will be the values at the end of each integration step, ending with the variable’s final value.
F.5.2.5 Formulating the Solution of IVODEs
Chapter 8.4 outlines a workflow for completing reaction engineering tasks or assignments that includes formulating the calculations for solving equations numerically. When solving IVODEs, the formulation of the calculations will include specifications for the derivatives function and specifications for a reactor function.
The specifications for the derivatives function should list the independent and dependent variables as its arguments and the corresponding derivatives of the dependent variables as its return variables. If any other input variables need to be made available to the derivatives function, its specifications should list them. The derivatives function specifications also should include an algorithm that lists a sequence of equations that can be used to calculate the derivatives starting from known constants, the independent and dependent variables and the variables that have been made available to the derivatives function.
The specifications for the reactor function may list arguments or it may indicate that it doesn’t take any arguments. More importantly, the specifications for the reactor function will list a set of corresponding values of the independent and dependent variables spanning the range from their initial to their final values as the return values. The algorithm will define the initial values and the stopping criterion, make variables listed in the derivatives function available to it, call the IVODE solver, and return the solution found by the solver. Before returning the solution, it should verify that the solver did not encounter any of the issues noted above
F.5.3 Solving DAEs
A set of IVODEs coupled to a set of ATEs comprise a set of DAEs. The numerical solution, then, is sets of corresponding values of the IVODE independent and dependent variables spanning the range from their initial to their final values togther with a set of values for the ATE variables that solve the ATEs.
To solve the DAEs encountered in Reaction Engineering Basics, a special DAE solver is not needed. They can be solved using an ATE solver and an IVODE solver. That means that both a residuals function and a derivatives function must be written when solving DAEs in Reaction Engineering Basics.
F.5.3.1 Using an ATE Solver and an IVODE Solver to Solve DAEs
It was noted previously that there are two situations where DAEs are encountered in Reaction Engineering Basics. In the first situation, either the initial value of a dependent variable or a constant in the IVODEs is an additional unknown, but two final values are known. The ATE in this situation is implicit. As an example, suppose that \(y_1\) and \(y_2\) are IVODE dependent variables with known final values of \(y_{1,f}\) and \(y_{2,f}\), and that \(C\) is the additional unknown (either an initial value or a constant appearing in the IVODEs). The ATE component of the DAEs can then be written as shown in Equation F.18 where \(C\) is the ATE variable. In effect it says \(C\) has the value that results in \(y_2 = y_{2,f}\) when the final value of \(y_1\) is \(y_{1,f}\).
\[ C \, : \, y_2\big\vert_{y_1 = y_{1,f}} = y_{2,f} \qquad \Rightarrow \qquad \epsilon_C = y_2\big\vert_{y_1 = y_{1,f}} - y_{2,f} \tag{F.18}\]
In the second situation, both the initial and final values of one or more dependent variables are unknown, but they are related through explicit ATEs. In this case, the unknown initial values should be used as the ATE variables. The unknown final values can then be treated as additional unknowns appearing in the ATEs.
In both situations, the key to solving the DAEs numerically is to call the ATE solver first. When the ATE residuals function is called, a guess for the ATE variables will be passed to it as its only argument. Using that guess, the IVODEs can then be solved within the residuals function. Using the results from solving the IVODEs, the residuals can be evaluated. After the ATE solver converges to a solution for the ATEs, the IVODEs can be solved a final time using that solution.
F.5.3.2 Formulating the Solution of DAEs
Chapter 8.4 outlines a workflow for completing reaction engineering tasks or assignments that includes formulating the calculations for solving equations numerically. When solving DAEs, the formulation of the calculations will include specifications for the residuals function, the derivatives function and a reactor function. The derivatives function specifications will be no different from when solving only IVODEs.
There are a few minor difference in the residuals function, compared to when solving ATEs. Specifically, the algorithm must begin by defining the initial values and stopping criterion for the IVODEs. If the ATE variable is a constant appearing in the IVODEs, the algorithm must also make that constant available to the derivatives function. Then it must call the IVODE solver and use the results it returns to calculate the ATE residuals.
The specifications for the reactor function are also slightly different compared to reactor functions for solving only ATEs or only IVODEs. The reactor function may or may not have any arguments. The return variables will be a set of ATE variables that solve the ATEs together with sets of corresponding values of the IVODE independent and dependent variables spanning the range from their initial to their final values. The algorithm for the reactor function will begin by defining a guess for the ATE variables and calling the ATE solver to get a solution of the ATEs. Then, using that solution, the initial values and stopping criterion for the IVODEs will be defined, and the IVODE solver will be called.
F.5.4 Solving BVODEs
A set of BVODEs applies in an interval of the independent variable, beginning at its lower bound (or lower limit) and ending at its upper bound. There will be \(N\) dependent variables and one independent variable in a set of \(N\) BVODEs. The numerical solution of a set of BVODEs consists of sets of values (i. e. vectors) of the independent variable and each dependent variable. The sets all contain the same number of values. The values of the independent variable begin at its lower bound and increase monotonically, ending at its upper bound. For each dependent variable, the nth value is the value of that dependent variable corresponding to the nth value of the independent variable. In other words, the numerical solution of a set of BVODEs consists of sets of corresponding values of the independent and dependent variables spanning the range from the lower bound of the independent variable to its upper bound. A BVODE solver is a computer function that solves a set of BVODEs numerically. This sub-appendix describes the input required by BVODE solvers, how they work, the results they return, and potential issues that can arise when using them.
F.5.4.1 BVODE Solver Input
Typically a BVODE solver must be provided with four inputs. The first is called the initial mesh and is described below. The second input is a guess for each of the dependent variables within the interval where the BVODEs apply as described below. The third and fourth inputs are a derivatives function and a boundary conditions residuals function. The order and formatting of the arguments and return values will vary from one software package to the next.
F.5.4.1.1 The Initial Mesh and Guess
The first input to a BVODE solver is called the initial mesh. The interval between the lower and upper bounds of the independent variable must be divided into \(N_i\) intervals. This requires \(N_i+1\) mesh points with the first being the lower bound and the last, the upper bound. The intervals between successive mesh points do not need to be equally sized. The engineer must choose \(N_i\), but typically it is not critical because the solver will adjust it.
Once an initial mesh has been defined, guesses for the values of each dependent variable at each mesh point are the second required input. That may seem like a large number of guesses, but often it is possible to get by with one of two simple guesses. The first simple guess is to simply set all of the dependent variables equal to zero at all mesh points. If the solver does not converge with that guess, a guess for the average value of each dependent variable over the entire mesh can be used as the guess for that dependent variable at each of the mesh points. Again, the specifics for providing the initial guess to the solver will depend upon the particular software package being used.
F.5.4.1.2 The Derivatives Function
The purpose of the derivatives function is to calculate the values of the derivatives at the mesh points, given the mesh points and the values of the dependent variables at the mesh points. The engineer solving the BVODEs must write the derivatives function, but because it will be called by the BVODE solver, the arguments to it and the values it returns are specified by the BVODE solver software package.
There are two common specifications for the arguments and return values for the derivatives function. Some software packages specify that the arguments are a single mesh point and the corresponding values of the dependent variables at that mesh point. In this case, the specified return values are the values of the derivatives at that one mesh point. Other software packages specify that the arguments are the full set of mesh points (typically in the form of a vector) and the full set of dependent variables values at those mesh points (typcially as a matrix). In this case the specified return values are the values of the derivatives at each of the mesh points (also typically as a matrix).
In Reaction Engineering Basics, BVODE solutions are formulated assuming that the arguments to the derivatives function are one of the mesh points along with the values of the dependent variables at that mesh point, and that the values of the derivative of each dependent variable with respect to the independent variable at that mesh point are returned. However each formulation in the book notes that some software packages may specify the full set of mesh points and the values of dependent variables at all of the mesh points as the arguments and the values of the derivatives at all of the mesh point as the return values.
In some situations, the derivatives function may need the values of variables other than those passed to it as arguments. Because the arguments are specified by the mathematics software package being used, any such quantities must be made available to the derivatives function by some other means than being passed to it as arguments.
F.5.4.1.3 The Boundary Conditions Residuals Function
Boundary conditions are ATEs that must be satisfied by the dependent variables at the upper and lower bounds of the independent variable. They must be written as residual expressions so that the third required input, the boundary conditions residuals function, can evaluate them, given the values of the dependent variables at the two bounds. As is the case for the derivatives function, the engineer solving the BVODEs must write the boundary conditions residuals function, but because it will be called by the BVODE solver, the arguments to it and the values it returns are specified by the BVODE solver software package.
BVODE solvers commonly specify that the arguments to the boundary conditions residuals function are the values of the dependent variables at each of the boundaries and the return values are the corresponding values of the residuals. The specifics of how these arguments and return values are formatted will again depend upon the software package being used. Very often the values of the dependent variables at each of the boundaries are passed to the boundary conditions residuals function as separate vectors while the residuals are returned as a single vector.
As with the derivatives function, the boundary conditions residuals function may need the values of variables other than those passed to it as arguments. Because the arguments are specified by the mathematics software package being used, any such quantities must be made available to the boundary conditions residuals function by some other means than being passed to it as arguments.
F.5.4.2 How BVODE Solvers Work
A BVODE solver solves the equations using a mesh where the span of the independent variable, \(z\) is divided into \(N_i\) intervals using \(N_i+1\) mesh points with \(z_1\) equal to the lower bound, \(z_{lb}\), and \(z_{N_i+1}\) equal to the upper bound, \(z_{ub}\). The intervals between successive mesh points do not need to be equally sized.
To simplify the notation, consider just one dependent variable, \(y\). Functions that contain undetermined coefficients are used to approximate \(y\) in each interval. Cubic polynomials are a common approximating function. When using a cubic polynomial as the approximating function, the value of \(y\) within the \(k^{th}\) interval (i. e. between \(z_k\) and \(z_{k+1}\)) is approximated by Equation F.19, and its derivative is used to approximate \(\frac{dy}{dz}\) within the \(k^{th}\) interval, Equation F.20.
\[ y = a_k z^3 + b_k z^2 + c_k z + d_k \,; \quad z_k \le z \le z_{k+1} \tag{F.19}\]
\[ \frac{dy}{dz} = 3 a_k z^2 + 2 b_k z + c_k \,; \quad z_k \le z \le z_{k+1} \tag{F.20}\]
If there are \(N_i\) intervals, this introduces \(4N_i\) undetermined coefficients, \(a_1\), \(b_1\), \(c_1\), and \(d_1\) through \(a_{N_i}\), \(b_{N_i}\), \(c_{N_i}\), and \(d_{N_i}\). Finding the values of those \(4N_i\) undetermined coefficients yields an approximation for \(y\) that spans the full interval from \(z=z_{lb}\) to \(z=z_{ub}\). Doing so requires a set of \(4N_i\) independent equations containing the undetermined coefficients.
Each of the interior mesh points, \(z_2\) through \(z_{N_i}\) is the end of one interval and the start of the next. To prevent the approximation of \(y\) from being discontinuous, at each interior mesh point, \(z_k\), the values of \(y\) predicted by the two approximating functions on either side of \(z_k\) are required to be equal. This results in \(N_i-1\) equations like that given in Equation F.21. In addition a boundary condition will provide an equation that contains the value of \(y\) at either \(z=z_{lb}\) or \(z=z_{ub}\). This gives a total of \(N_i\) equations containing the \(4N_i\) undetermined coefficients.
\[ \begin{align} a_{k-1} z_k^3 &+ b_{k-1} z_k^2 + c_{k-1} z_k + d_{k-1} \\&= a_k z_k^3 + b_k z_k^2 + c_k z_k + d_k \end{align} \qquad k = 2, 3, \cdots, N_i \tag{F.21}\]
To generate \(3N_i\) additional equations, three collocation points are chosen within each interval. Typically the two end points and the mid-point of the interval are used. At each of these collocation points, the derivatives function can be used to calculate \(\frac{dy}{dz}\) which then can be substituted in Equation F.20. Doing this at three collocation points within each interval brings the total number of equations to \(4N_i\).
The \(4N_i\) equations containing the \(4N_i\) undetermined coefficients are non-linear, so they are solved numerically to find the values of the coefficients, \(a_1\), \(b_1\), \(c_1\), and \(d_1\) through \(a_{N_i}\), \(b_{N_i}\), \(c_{N_i}\), and \(d_{N_i}\). Converting the initial guess for the dependent variables at the mesh points (one of the BVODE arguments) to initial guesses for these coefficients is handled internally by the BVODE solver, as is solving the equations to find the coefficients.
When solving a set of BVODEs, there will be multiple dependent variables, and the approach outlined here is applied to each dependent variable. Typically the BVODE solver will adjust the number of intervals used in the calculations to ensure an accurate solution.
F.5.4.3 BVODE Solver Issues
Effectively the BVODE solver converts the ODEs into ATEs and solves the ATEs. As such, a BVODE solver may encounter the same issues as an ATE solver. In addition, the mesh is used to convert the ODEs into ATEs, and this can cause issues. Specifically, if a dependent variable changes over a small sub-interval of the independent variable, more mesh points may be needed in that sub-interval than in intervals were the change in the dependent variable is smaller. If such an issue arises, the number and spacing of the initial mesh points can be adjusted.
F.5.4.4 BVODE Solver Return Values
As noted above, the solution of a set of BVODEs is a set of corresponding values of the independent and dependent variables spanning the range from the lower bound of the independent variable to its upper bound. The number of values in each set is not known because the solver may change both the number of mesh points and their locations as it solves the equations. Nonetheless, the first value will correspond to the lower bound and the last, to the upper bound.
F.5.4.5 Formulating the Solution of BVODEs
Using the assignment completion workflow described in Chapter 8.4, will require writing specifications for the derivatives function and the boundary conditions residuals function. The specifications for the derivatives function are essentially the same as when solving IVODEs. They should list the arguments passed to it, quantities that must be made available to it by other means, the quantities it returns, and its algorithm. As already noted, the arguments might be the independent and dependent variables for a single mesh point, or they might be for all of the mesh points, depending on the solver being used. The algorithm should calculate any additional unknowns and the evaluate and return the derivatives at the mesh point(s) passed to the function.
The specifications for the boundary conditions residuals function should similarly list the dependent variables at the upper and lower bounds as its arguments. Quantities that must be made available to it by other means should be listed. The boundary conditions residuals calculated using the argument should be liste as the return values. The algorithm should consist of residual expressions corresponding to the boundary conditions.
F.6 Estimating Parameters
Parameter estimation involves using experimental data to find the best values for unknown, constant parameters appearing in a model of the experiments that generated the experimental data. This is sometimes called fitting the model to the data. In each experiment, the values of one or more adjusted experimental input variables are set by the person doing the experiments, and then the value of an experimental response is measured. In Reaction Engineering Basics only experiments with a single experimental response are considered. Every experiment that is performed involves the same set of adjusted input variables and the same experimental response, but their values are different from experiment to experiment.
Most readers of Reaction Engineering Basics will be familiar fitting a linear model to experimental data using least squares. This can be done using a calculator, a spreadsheet, or a least-squares fitting function from a mathematics software package. Fitting linear models to experimental data is not considered in this appendix. Here the focus is on using numerical methods to fit arbitrary models to experimental data. The models may include numerical solution of sets of equations as described above. The computer functions from mathematics software packages that are used to fit models to data will be referred to here as fitting functions.
F.6.1 Fitting Function Input
Generally a fitting function must be provided with four inputs. The first is an initial guess for the parameters being estimated, the second is the values of the adjusted input variables for each of the experiments in the data set, the third is the corresponding values of the experimental response for each experiment, and the fourth is a predicted response function.
F.6.1.1 The Initial Guess for the Parameters being Estimated
Guessing values for the parameters being estimated can be challenging. Typically the engineer does not have any idea what the value may be, and for some parameters the range of possible values can span ten orders of magnitude or more. In this situation, if the initial guess is not sufficiently close to the actual value of the parameter, the fitting function may fail to converge because it is not making progress. One way to reduce the likelihood of this happening is to use the base-10 logarithm of the parameter instead of the parameter itself. That is, if \(k_0\) is the actual parameter of interest in the model, re-write the model replacing \(k_0\) with \(10^\beta\). Then perform parameter estimation to find the best value of \(\beta\). When the possible range of \(k_0\) is between 10-20 and 1020, the corresponding range of \(\beta\) is between -20 and 20, making it easier to guess. Once the best value \(\beta\) has been found, the best value of \(k_0\) is simply calculated as \(k_0 = 10^\beta\). This approach is illustrated in Example 18.6.2.
F.6.1.2 The Experimental Data
The adjusted experimental inputs and the corresponding experimental response for the experiment are typically available as a table or spreadsheet file. This makes it easy to create a matrix containing the experimental inputs and a vector containing the corresponding experimental responses. Those are the formats most often used to pass the experimental inputs and responses to the fitting function.
F.6.1.3 The Predicted Responses Function
The purpose of the predicted response function is to calculate the experimental responses predicted by the model for each experiment, given a guess for the values of the parameters. The predicted responses function is written by the engineer, but it is called by the numericaly fitting function. For this reason, the software package that provides the numerical fitting function specifies arguments that must be provided to the predicted responses function, the form in which they are provided, the values returned by the fitting function, and the form in which they are returned. Nonetheless, the arguments to the predicted responses function will include values for the model parameters and the set of adjusted experimental inputs from all of the experiments. The predicted responses function will return the set of model-predicted responses for all of the experiments.
Calculating the model-predicted response for each experiment will typically entail solving the reactor design equations for the reactor used in the experiments. The reactor design equations will usually be ATEs or IVODEs. Consequently, the algorithm for the predicted responses function will typically include calling a reactor function, and the reactor function will call an appropriate equation solver.
F.6.2 How Fitting Functions Work
A fitting function works in much the same manner as an ATE solver (see Section F.5.1) except that instead of finding values of unknowns that cause a set of residuals to equal zero it finds values of model parameters that minimize the sum of the squares of the errors between the experimental responses and the model-predicted responses, Equation F.22.
\[ \Psi = \sum_i \left( y_{i,expt} - y_{i,model} \right)^2 \tag{F.22}\]
In essence, the fitting function finds the best parameter values by trial and error.
- Using the initial guess for the model parameters, it calls the predicted responses function to get the model-predicted responses and then calculates \(\Psi\) using Equation F.22.
- It saves the initial guess and the corresponding \(\Psi\) as the best values.
- It repeatedly
- generates an improved guess
- calculates \(\Psi\) as above, and
- if \(\Psi\) is less than the best \(\Psi\) it saves the improved guess and corresponding \(\Psi\) as the best values.
- It stops generating new guesses when it is unable to generate an improved guess that results in a smaller \(\Psi\).
F.6.3 Fitting Function Issues
Parameter estimation as described above is an iterative process. Ideally, as the fitting function generates improved guesses, the corresponding sum of the squares of the errors gets smaller and smaller. This is called convergence. The fitting function uses a set of convergence criteria to determine when it stops generating guesses and returns the current best values. A few possible issues should be kept in mind when performing numerical parameter estimation. The first is that the fitting function may converge to a local minimum of the sum of the squares of the errors and not the global minimum. In this situation, the fitting function would return a flag indicating that it converged (see return values, below), but the results would likely indicate that the model is not accurate. The apparent inaccuracy, though, is due to convergence to a local minimum and not necessariy due to the model. That is, if the fitting function converged to the global minimum, the model might actually prove to be quite accurate. One way to try to detect this situation is to repeat the parameter estimation using a very different initial guess. If the solver converges to a different set of estimated parameters, that indicates that one (or possibly both) of the sets of estimated parameters corresponds to a local minimum. If a wide range of initial guesses always leads to the same parameter estimates, that may suggest the a global minimum has been found.
The second issue arises when the experimental responses span several orders of magnitude. In this situation, the value of the sum of the squares of the errors, \(\Psi\) in Equation F.22, may be dominated by the responses with the greater magnitude. This can result in a fitted model that is accurate under conditions where the response is larger, but less accurate when the response is smaller. One way to address this is to minimize the sum of the squares of the relative errors, Equation F.23, instead of the sum of the squares of the absolute errors, Equation F.22.
\[ \Psi = \sum_i \left( \frac{ y_{i,expt} - y_{i,model}}{y_{i,expt}} \right)^2 \tag{F.23}\]
F.6.4 Fitting Function Return Values
The fitting function will return the best estimates for the parameters that it was able to find. Typically it will aslo return a flag or message that indicates whether it converged and why it stopped iterating. Most fitting functions can also be made to return a variety of other variables. In most cases the mathematics software package being used will describe how to cause the fitting function to also return the coefficient of determination, \(R^2\), and either the standard error or the 95% confidence interval for each parameter.
F.6.5 Assessing the Accuracy of the Fitted Model
The fitting function will return the best estimates for the parameters in the model, but that does not necessarily result in an accurate model. The mathematical form of the model may be incapable predicting the variation of the experimental responses no matter what values are used for the parameters. For this reason, it is necessary to assess the accuracy of the fitted model.
There are several statistical indicators that a fitted model accurately represents the data to which it was fit. First, the coefficient of determination, \(R^2\), will be close to 1. The uncertainty in most of the estimated parameters, if not all, will be small relative to the extimated value. That is, the standard error for the parameter will be small compated to the value of the parameter or the upper and lower limits of the 95% confidence interval will be close to the estimated value of the parameter.
As noted in Chapter 18, there could be a few paramters for which the uncertainty is large but the model is still accurate. This could indicate one of three possibilities. First, the values to which the adjusted input variables were set in the experiments may not allow accurate resolution of those parameters that have high uncertainty. Second, parameters with higher uncertainty may be mathematically coupled to each other (e. g. the model-predicted response may only depend on the product of two parameters so that the individual parameters can have any values as long as their product has the optimum value). Third, the parameters with high uncertainty may not be needed, and there may be a simpler model with fewer parameters that is equally accurate.
Two different kinds of graphs are helpful when assessing the accuracy of a numerical model. The first is callea a parity plot. In a parity plot the model-predicted responses are plotted versus the experimental responses as data points. The parity line, \(y_{expt} = y_{model}\), is then added to the graph. If there were no random errors in the experimental data and the model was exact, then every experimental data point in a parity plot would fall on the parity line. If the model is accurate, the deviations from data from the parity line will be small.
The second type of graph used with numerical models is called a residuals plot. The experiment residuals are the differences between the experimental responses and the model-predicted responses for the set of experiments, Equation F.24. A set of residuals plots can be created wherein the residuals are plotted versus each of the experimental adjusted input variables. If there were no random errors in the experimental data and the model was exact, then every experiment residual would equal zero and fall on the horizontal axis. If there are trends in the deviations of the experiment residuals, it may indicate that the model does not fully capture the effect of the plotted experimental input upon the response.
\[ \epsilon_{expt,i} = y_{i,expt} - y_{i,model} \tag{F.24}\]
In Reaction Engineering Basics experiment residuals are only plotted against each of the adjusted inputs. However, a residuals plot can be generated for any aspect of the experiments that might affect the results of an experiment. For example the experiment residuals could be plotted against the vendor from whom a reagent was purchased to see whether the source of the reagent was affecting the results.
Ultimately, deciding whether the model is sufficiently accurate is a judgement call. To summarize, the following criteria are satisfied by an accurate model.
- The coefficient of determination, \(R^2\), is nearly equal to 1.
- The uncertainty in most, if not all, of model parameters is small compared to the parameter’s value.
- When using standard errors of the parameters, they are small compared to the parameter value.
- When using 95% confidence intervals, the upper and lower limits of the interval are close to the parameter value.
- The points in the parity plot are all close to a diagonal line passing through the origin.
- In each residuals plot, the points scatter randomly about the horizontal axis, and no systematic deviations are apparent.
F.6.6 Formulating the Fitting of a Model to Experimental Data
Using the assignment completion workflow described in Chapter 8.4, will require writing specifications for the predicted responses function and an estimated parameters function.
The specifications for the predicted responses function will list the adjusted experimental inputs and a guess for the parameters to be estimated as the arguments and the model predicted responses as the return variables. The algorithm will loop through the experiments. For each experiment it will typically call a reactor model to solve the design equations for the reactor and then use the results to calculate the predicted response. When analyzing kinetics data, the reactor model will typically be a set of ATEs or IVODEs, and the reactor function will call either a residuals function or a derivatives function. In this situation, the predicted responses function algorithm must make the parameters to be estimated available to the residuals or derivatives function before calling the reactor function.
The estimated parameters function specifications will list the adjusted experimental inputs and the experimental responses as arguments. The return variables will be the best estimates for the parameters being estimated, the standard error or the 95% confidence intervals for the parameter estimates, and the coefficient of determination. The algorithm will define an intial guess for the parameters to be estimated and then call the fitting function. Before returning the results, it should check that the fitting function converged.
F.7 Symbols Used in This Appendix
| Symbol | Meaning |
|---|---|
| \(a_i\) | Undetermined coefficient in a cubic approximating polynomial. |
| \(b_i\) | Undetermined coefficient in a cubic approximating polynomial. |
| \(c_i\) | Undetermined coefficient in a cubic approximating polynomial. |
| \(d_i\) | Undetermined coefficient in a cubic approximating polynomial. |
| \(f_j\) | Derivative function. |
| \(g_j\) | Function of the independent and dependent variables in a general set of ODEs. |
| \(_{lb}\) | Subscript denoting the lower bound. |
| \(m_{i,j}\) | Coefficient in the matrix form of a set of differential equations. |
| \(\dot{n}_{i,k}\) | Molar flow rate of reagent \(i\) in flow stream \(k\). |
| \(r\) | Reaction rate. |
| \(t\) | Time. |
| \(_{ub}\) | Subscript denoting the upper bound. |
| \(y_i\) | Dependent variable in a general set of ODEs. |
| \(z\) | Independent variable in a general set of ODEs or distance from the reactor inlet. |
| \(C\) | Unknown IVODE constant or initial value. |
| \(C_{i,k}\) | Concentration of reagent \(i\) in flow stream \(k\). |
| \(\boldsymbol{M}\) | Mass matrix. |
| \(N\) | Number of equations. |
| \(N_i\) | Number of intervals in a BVODE mesh. |
| \(R^2\) | Coefficient of determination. |
| \(V\) | Reacting fluid volume. |
| \(\dot{V}\) | Volumetric flow rate. |
| \(\epsilon\) | Residual. |
| \(\Delta z\) | Integration step size. |
| \(\Psi\) | Sum of the squares of the errors. |